Question
The percentage of pyridine $$\left( {{C_5}{H_5}N} \right)$$ that forms pyridinium ion $$\left( {{C_5}{H_5}{N^ + }H} \right)$$ in a $$0.10\,M$$ aqueous pyridine solution ( $${K_b}$$ for $${C_5}{H_5}N = 1.7 \times {10^{ - 9}}$$ ) is
A.
0.0060%
B.
0.013%
C.
0.77%
D.
1.6%
Answer :
0.013%
Solution :
The percentage of pyridine can be equal to the percentage of dissociation of pyridinium ion and pyridine solution as shown below :
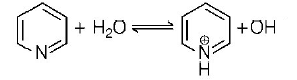
As pyridinium is a weak base, so degree of dissociation is given as
$$\eqalign{ & \alpha = \sqrt {\frac{{{K_b}}}{C}} \cr & \,\,\,\,\, = \sqrt {\frac{{1.7 \times {{10}^{ - 9}}}}{{0.10}}} \cr & \,\,\,\,\, = \sqrt {1.7 \times {{10}^{ - 8}}} \cr & \,\,\,\,\, = 1.3 \times {10^{ - 4}} \cr & {\text{or, percentage of dissociation}} \cr & = \left( {\alpha \times 100} \right)\% \cr & = \left( {1.3 \times {{10}^{ - 4}}} \right) \times 100 \cr & = 0.013\% \cr} $$
The percentage of pyridine can be equal to the percentage of dissociation of pyridinium ion and pyridine solution as shown below :
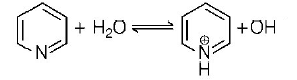
As pyridinium is a weak base, so degree of dissociation is given as
$$\eqalign{ & \alpha = \sqrt {\frac{{{K_b}}}{C}} \cr & \,\,\,\,\, = \sqrt {\frac{{1.7 \times {{10}^{ - 9}}}}{{0.10}}} \cr & \,\,\,\,\, = \sqrt {1.7 \times {{10}^{ - 8}}} \cr & \,\,\,\,\, = 1.3 \times {10^{ - 4}} \cr & {\text{or, percentage of dissociation}} \cr & = \left( {\alpha \times 100} \right)\% \cr & = \left( {1.3 \times {{10}^{ - 4}}} \right) \times 100 \cr & = 0.013\% \cr} $$