Question
The $$d$$-electron configurations of $$C{r^{2 + }},M{n^{2 + }}\,F{e^{2 + }}$$ and $$C{o^{2 + }}$$ are $${d^4},{d^5},{d^6}$$ and $${d^7}$$ respectively. Which one of the following will exhibit minimum paramagnetic behaviour?
The $$d$$-electron configurations of $$C{r^{2 + }},M{n^{2 + }}\,F{e^{2 + }}$$ and $$C{o^{2 + }}$$ are $${d^4},{d^5},{d^6}$$ and $${d^7}$$ respectively. Which one of the following will exhibit minimum paramagnetic behaviour?
$$\left( {{\text{At}}{\text{.}}\,{\text{no}}{\text{.}}\,Cr = 24,Mn = 25,} \right.$$ $$\left. {Fe = 26,Co = 27} \right)$$
A.
$${\left[ {Fe{{\left( {{H_2}O} \right)}_6}} \right]^{2 + }}$$
B.
$${\left[ {Co{{\left( {{H_2}O} \right)}_6}} \right]^{2 + }}$$
C.
$${\left[ {Cr{{\left( {{H_2}O} \right)}_6}} \right]^{2 + }}$$
D.
$${\left[ {Mn{{\left( {{H_2}O} \right)}_6}} \right]^{2 + }}$$
Answer :
$${\left[ {Co{{\left( {{H_2}O} \right)}_6}} \right]^{2 + }}$$
Solution :
$$C{r^{2 + }}:{d^4}$$
($$4$$ unpaired electrons)
$$M{n^{2 + }}:{d^5}$$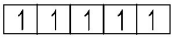
($$5$$ unpaired electrons)
$$F{e^{2 + }}:{d^6}$$
($$4$$ unpaired electrons)
$$C{o^{2 + }}:{d^7}$$
($$3$$ unpaired electrons)
∴ $${\left[ {Co{{\left( {{H_2}O} \right)}_6}} \right]^{2 + }}$$ has minimum number of unpaired electrons and thus, shows minimum paramagnetic behaviour.
Higher the unpaired $${e^ - }.$$
Higher the magnetic moment
$$\mu = \sqrt {n\left( {n + 2} \right)} $$
$$n=$$ Number of unpaired $${e^ - }$$
$$C{r^{2 + }}:{d^4}$$
($$4$$ unpaired electrons)$$M{n^{2 + }}:{d^5}$$
($$5$$ unpaired electrons)$$F{e^{2 + }}:{d^6}$$
($$4$$ unpaired electrons)$$C{o^{2 + }}:{d^7}$$
($$3$$ unpaired electrons)∴ $${\left[ {Co{{\left( {{H_2}O} \right)}_6}} \right]^{2 + }}$$ has minimum number of unpaired electrons and thus, shows minimum paramagnetic behaviour.
Higher the unpaired $${e^ - }.$$
Higher the magnetic moment
$$\mu = \sqrt {n\left( {n + 2} \right)} $$
$$n=$$ Number of unpaired $${e^ - }$$