Question
The activation energy of a reaction can be determined from the slope of which of the following graphs?
A.
$${\text{ln}}\,K\,{\text{vs}}\,T$$
B.
$$\frac{{{\text{ln}}\,K}}{T}\,{\text{vs}}\,T$$
C.
$${\text{ln}}\,K\,{\text{vs}}\,\frac{l}{T}$$
D.
$$\frac{T}{{{\text{ln}}\,K}}\,{\text{vs}}\,\frac{l}{T}$$
Answer :
$${\text{ln}}\,K\,{\text{vs}}\,\frac{l}{T}$$
Solution :
$$\eqalign{ & {\text{By Arrhenius equation}} \cr & K = A{e^{ - \,\frac{{Ea}}{{RT}}}} \cr & {\text{where,}}\,{E_a} = {\text{energy of activation}} \cr & {\text{Applying log on both the side,}} \cr & {\text{ln}}\,k = {\text{ln}}A - \frac{{{E_a}}}{{RT}}\,\,\,...\left( {\text{i}} \right) \cr & {\text{or}}\,\,\,{\text{log}}\,k = - \frac{{{E_a}}}{{2.303\,RT}} + {\text{log}}\,A\,\,\,...\left( {{\text{ii}}} \right) \cr} $$
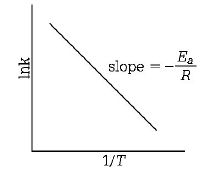
Compare the above equation $$w.r.t.$$ straight line equation of $$y = mx + c.$$ Thus, if a plote of $${\text{ln}}\,k\,\,{\text{vs}}\,\frac{1}{T}$$ is a straight line, the validity of the equation is confirmed.
Slope of the line $$ = - \frac{{{E_a}}}{R}$$
Thus, measuring the slope of the line, the value of $${{E_a}}$$ can be calculated.
$$\eqalign{ & {\text{By Arrhenius equation}} \cr & K = A{e^{ - \,\frac{{Ea}}{{RT}}}} \cr & {\text{where,}}\,{E_a} = {\text{energy of activation}} \cr & {\text{Applying log on both the side,}} \cr & {\text{ln}}\,k = {\text{ln}}A - \frac{{{E_a}}}{{RT}}\,\,\,...\left( {\text{i}} \right) \cr & {\text{or}}\,\,\,{\text{log}}\,k = - \frac{{{E_a}}}{{2.303\,RT}} + {\text{log}}\,A\,\,\,...\left( {{\text{ii}}} \right) \cr} $$
Compare the above equation $$w.r.t.$$ straight line equation of $$y = mx + c.$$ Thus, if a plote of $${\text{ln}}\,k\,\,{\text{vs}}\,\frac{1}{T}$$ is a straight line, the validity of the equation is confirmed.
Slope of the line $$ = - \frac{{{E_a}}}{R}$$
Thus, measuring the slope of the line, the value of $${{E_a}}$$ can be calculated.
