191.
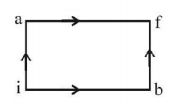
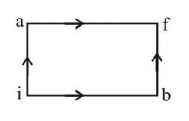
When a system is taken from state $$i$$ to state $$f$$ along the path $$iaf,$$ it is found that $$Q = 50\,cal$$ and $$W = 20\,cal.$$ Along the path $$ibf\,Q = 36\,cal.$$ $$W$$ along the path $$ibf$$ is
A
$$14\,cal$$
B
$$6\,cal$$
C
$$16\,cal$$
D
$$66\,cal$$
Answer :
$$6\,cal$$
192. The mass of a hydrogen molecule is $$3.32 \times {10^{ - 27}}\,kg.$$ If $${10^{23}}$$ hydrogen molecules strike, per second, a fixed wall of area $$2\,c{m^2}$$ at an angle of 45° to the normal, and rebound elastically with a speed of $${10^3}\,m/s,$$ then the pressure on the wall is nearly :
A
$$2.35 \times {10^3}\,N/{m^2}$$
B
$$4.70 \times {10^3}\,N/{m^2}$$
C
$$2.35 \times {10^2}\,N/{m^2}$$
D
$$4.70 \times {10^2}\,N/{m^2}$$
Answer :
$$2.35 \times {10^3}\,N/{m^2}$$
193. The temperature of source and sink of a heat engine are $${127^ \circ }C$$ and $${27^ \circ }C$$ respectively. An inventor claims its efficiency to be $$26\% ,$$ then:
A
it is impossible
B
it is possible with high probability
C
it is possible with low probability
D
data are insufficient.
Answer :
it is impossible
194. For a certain gas the ratio of specific heats is given to be $$\gamma = 1.5,$$ for this gas
A
$${C_V} = \frac{{3R}}{J}$$
B
$${C_p} = \frac{{3R}}{J}$$
C
$${C_p} = \frac{{5R}}{J}$$
D
$${C_v} = \frac{{5R}}{J}$$
Answer :
$${C_p} = \frac{{3R}}{J}$$
195.
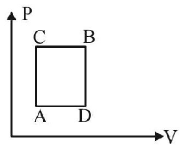
A gas can be taken from $$A$$ to $$B$$ via two different processes $$ACB$$ and $$ADB.$$
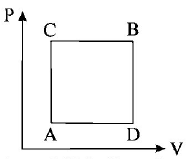
When path $$ACB$$ is used 60$$J$$ of heat flows into the system and 30 $$J$$ of work is done by the system. If path $$ADB$$ is used
work done by the system is 10 $$J.$$ The heat Flow into the system in path $$ADB$$ is :
A
40 $$J$$
B
80 $$J$$
C
100 $$J$$
D
20 $$J$$
Answer :
40 $$J$$
196. If an air conditioner is put in the middle of a room and started working
A
the room can be cooled slightly
B
the temperature of the room will not change
C
the room will become slightly warmer
D
the same temperature will be attained in the room as by putting it on the window in the standard position
Answer :
the room will become slightly warmer
197. The molar specific heat at constant pressure of an ideal gas is $$\left( {\frac{7}{2}} \right)R.$$ The ratio of specific heat at constant pressure to that at constant volume is
A
$$\frac{7}{5}$$
B
$$\frac{8}{7}$$
C
$$\frac{5}{7}$$
D
$$\frac{9}{7}$$
Answer :
$$\frac{7}{5}$$
198. The specific heat of a gas at constant pressure is greater than the specific heat of the same gas at constant volume because
A
work is done in the expansion of the gas at constant pressure.
B
work is done in the expansion of the gas at constant volume.
C
the attraction between the molecules increases at constant pressure.
D
the molecular attraction increases at constant volume.
Answer :
work is done in the expansion of the gas at constant pressure.
199. Two thermally insulated vessels 1 and 2 are filled with air at temperatures $$\left( {{T_1},{T_2}} \right),$$ volume $$\left( {{V_1},{V_2}} \right)$$ and pressure $$\left( {{P_1},{P_2}} \right)$$ respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
A
$$\frac{{{T_1}{T_2}\left( {{P_1}{V_1} + {P_2}{V_2}} \right)}}{{\left( {{P_1}{V_1}{T_2} + {P_2}{V_2}{T_1}} \right)}}$$
B
$${\frac{{\left( {{T_1} + {T_2}} \right)}}{2}}$$
C
$${{T_1} + {T_2}}$$
D
$$\frac{{{T_1}{T_2}\left( {{P_1}{V_1} + {P_2}{V_2}} \right)}}{{\left( {{P_1}{V_1}{T_1} + {P_2}{V_2}{T_2}} \right)}}$$
Answer :
$$\frac{{{T_1}{T_2}\left( {{P_1}{V_1} + {P_2}{V_2}} \right)}}{{\left( {{P_1}{V_1}{T_2} + {P_2}{V_2}{T_1}} \right)}}$$
200.
For an ideal gas graph is shown for three processes. Process 1, 2 and 3 are respectively.
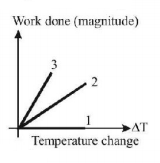
A
Isobaric, adiabatic, isochoric
B
Adiabatic, isobaric, isochoric
C
Isochoric, adiabatic, isobaric
D
Isochoric, isobaric, adiabatic
Answer :
Isochoric, isobaric, adiabatic