81. A Carnot engine is working between $${127^ \circ }C$$ and $${27^ \circ }C.$$ The increase in efficiency will be maximum when the temperature of
A
the source is increased by $${50^ \circ }C$$
B
the sink is decreased by $${50^ \circ }C$$
C
source is increased by $${25^ \circ }C$$ and that of sink is decreased by $${25^ \circ }C$$
D
both source and sink are decreased by $${25^ \circ }C$$ each.
Answer :
the sink is decreased by $${50^ \circ }C$$
82. 110 joules of heat is added to a gaseous system, whose internal energy is $$40\,J;$$ then the amount of external work done is
A
$$150\,J$$
B
$$70\,J$$
C
$$110\,J$$
D
$$40\,J$$
Answer :
$$70\,J$$
83.
A gas is taken through the cycle $$A \to B \to C \to A,$$ as shown. What is the net work done by the gas?

A
$$2000\,J$$
B
$$1000\,J$$
C
Zero
D
$$-2000\,J$$
Answer :
$$1000\,J$$
84. A closed system undergoes a process $$1 \to 2$$ for which the values $${W_{1 - 2}}$$ and $${Q_{1 - 2}}$$ are $$50\,kJ$$ and $$- 20\,kJ$$ respectively. If the system is returned to state 1 and $${Q_{2 \to 1}}$$ is $$+ 10\,kJ$$ the work done $${W_{2 \to 1}}$$ is
A
$$40\,kJ$$
B
$$50\,kJ$$
C
$$-60\,kJ$$
D
$$-50\,kJ$$
Answer :
$$-60\,kJ$$
85.
A thermodynamic system undergoes cyclic process $$ABCDA$$ as shown in figure. The work done by the system in the cycle is

A
$${p_0}{V_0}$$
B
$$2{p_0}{V_0}$$
C
$$\frac{{{p_0}{V_0}}}{2}$$
D
zero
Answer :
zero
86.
One mole of a diatomic ideal gas undergoes a cyclic process $$ABC$$ as shown in figure. The process $$BC$$ is adiabatic. The temperatures at $$A, B$$ and $$C$$ are 400 $$K,$$ 800 $$K$$ and 600 $$K$$ respectively. Choose the correct statement :

A
The change in internal energy in whole cyclic process is
250 $$R.$$
B
The change in internal energy in the process $$CA$$ is 700 $$R.$$
C
The change in internal energy in the process $$AB$$ is $$- 350\,R.$$
D
The change in internal energy in the process $$BC$$ is $$- 500\,R.$$
Answer :
The change in internal energy in the process $$BC$$ is $$- 500\,R.$$
87. A gas is compressed from a volume of $$2{m^3}$$ to a volume of $$1{m^3}$$ at a constant pressure of $$100\,N/{m^2}.$$ Then it is heated at constant volume by supplying $$150\,J$$ of energy. As a result, the internal energy of the gas:
A
increases by $$250\,J$$
B
decreases by $$250\,J$$
C
increases by $$50\,J$$
D
decreases by $$50\,J$$
Answer :
increases by $$250\,J$$
88. In thermodynamic processes which of the following statements is not true ?
A
In an adiabatic process the system is insulated from the surroundings
B
In an isochoric process pressure remains constant
C
In an isothermal process the temperature remains constant
D
In an adiabatic process $$p{V^\gamma } = {\text{constant}}$$
Answer :
In an isochoric process pressure remains constant
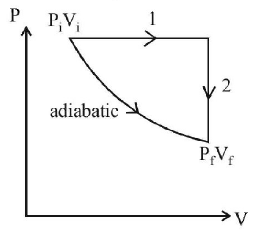
89. A gas is enclosed in a cylinder with a movable frictionless piston. Its initial thermodynamic state at pressure $${P_i} = {10^5}$$ $$Pa$$ and volume $${V_i} = {10^{ - 3}}{m^3}$$ changes to a final state at $${P_f} = \left( {\frac{1}{{32}}} \right) \times {10^5}$$ $$Pa$$ and $${V_f} = 8 \times {10^{ - 3}}{m^3}$$ in an adiabatic quasi - static process, such that $${P^3}{V^5}$$ = constant. Consider another thermodynamic process that brings the system from the same initial state to the same final state in two steps: an isobaric expansion at $${P_i}$$ followed by an isochoric (isovolumetric) process at volume $${V_f}.$$ The amount of heat supplied to the system in the two - step process is approximately
A
$$112\, J$$
B
$$294\, J$$
C
$$588\, J$$
D
$$813\, J$$
Answer :
$$588\, J$$
90. The specific heat of a gas in an isothermal process is
A
infinite
B
zero
C
negative
D
remains constant
Answer :
infinite