71.
A central particle $$M$$ is surrounded by a square array of other particles, separated by either distance $$d$$ or distance $$\frac{d}{2}$$ along the perimeter of the square. The magnitude of the gravitational force on the central particle due to the other particles is

A
$$\frac{{9GMm}}{{{d^2}}}$$
B
$$\frac{{5GMm}}{{{d^2}}}$$
C
$$\frac{{3GMm}}{{{d^2}}}$$
D
$$\frac{{GMm}}{{{d^2}}}$$
Answer :
$$\frac{{3GMm}}{{{d^2}}}$$
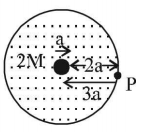
72. A solid sphere of mass $$'M\,'$$ and radius $$'a\,'$$ is surrounded by a uniform concentric spherical shell of thickness $$2a$$ and mass $$2M.$$ The gravitational field at distance $$'3a\,'$$ from the centre will be:
A
$$\frac{{2GM}}{{9{a^2}}}$$
B
$$\frac{{GM}}{{9{a^2}}}$$
C
$$\frac{{GM}}{{3{a^2}}}$$
D
$$\frac{{2GM}}{{3{a^2}}}$$
Answer :
$$\frac{{GM}}{{3{a^2}}}$$
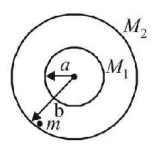
73.
Two concentric uniform shells of mass $${M_1}$$ and $${M_2}$$ are as shown in the figure. A particle of mass $$m$$ is located just within the shell $${M_2}$$ on its inner surface. Gravitational force on $$'m'$$ due to $${M_1}$$ and $${M_2}$$ will be
A
zero
B
$$\frac{{G{M_1}m}}{{{b^2}}}$$
C
$$\frac{{G\left( {{M_1} + {M_2}} \right)m}}{{{b^2}}}$$
D
None of these
Answer :
$$\frac{{G{M_1}m}}{{{b^2}}}$$
74. The period of revolution of the planet $$A$$ round the sun is 8 times that of $$B.$$ The distance of $$A$$ from the sun is how many times greater than that of $$B$$ from the sun?
A
5
B
4
C
3
D
2
Answer :
4
75. The gravitational field due to a mass distribution is $$E = \frac{K}{{{x^3}}}$$ in the $$x$$-direction. ($$K$$ is a constant). Taking the gravitational potential to be zero at infinity, its value at a distance $$x$$ is
A
$$\frac{K}{x}$$
B
$$\frac{K}{{2x}}$$
C
$$\frac{K}{{{x^2}}}$$
D
$$\frac{K}{{2{x^2}}}$$
Answer :
$$\frac{K}{{2{x^2}}}$$
76. If the earth were to rotates faster than its present speed, the weight of an object will
A
increase at the equator but remain unchanged at the poles
B
decrease at the equator but remain unchanged at the poles
C
remain unchanged at the equator but decrease at the poles
D
remain unchanged at the equator but increase at the poles
Answer :
decrease at the equator but remain unchanged at the poles
77. If $$g$$ is the acceleration due to gravity on the earth’s surface, the gain in the potential energy of an object of mass $$m$$ raised from the surface of the earth to a height equal to the radius $$R$$ of the earth, is-
A
$$\frac{1}{2}\,mgR$$
B
$$2\,mgR$$
C
$$mgR$$
D
$$\frac{1}{4}mgR$$
Answer :
$$\frac{1}{2}\,mgR$$
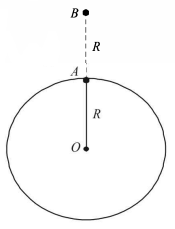
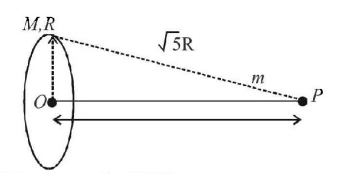
78. A point $$P$$ lies on the axis of a fixed ring of mass $$M$$ and radius $$R,$$ at a distance $$2R$$ from its centre $$O.$$ A small particle starts from $$P$$ and reaches $$O$$ under gravitational attraction only. Its speed at O will be
A
zero
B
$$\sqrt {\frac{{2GM}}{R}} $$
C
$$\sqrt {\frac{{2GM}}{R}\left( {\sqrt 5 - 1} \right)} $$
D
$$\sqrt {\frac{{2GM}}{R}\left( {1 - \frac{1}{{\sqrt 5 }}} \right)} $$
Answer :
$$\sqrt {\frac{{2GM}}{R}\left( {1 - \frac{1}{{\sqrt 5 }}} \right)} $$
79. The acceleration due to gravity on the planet $$A$$ is 9 times the acceleration due to gravity on the planet $$B.$$ A man jumps to a height of $$2\,m$$ on the surface of $$A.$$ What is the height of jump by the same person on the planet $$B$$ ?
A
$$6\,m$$
B
$$\frac{2}{3}\,m$$
C
$$\frac{2}{9}\,m$$
D
$$18\,m$$
Answer :
$$18\,m$$
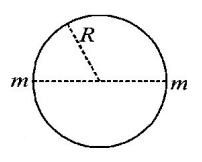
80. Two particles of equal mass $$'m'$$ go around a circle of radius $$R$$ under the action of their mutual gravitational attraction. The speed of each particle with respect to their centre of mass is
A
$$\sqrt {\frac{{Gm}}{{4R}}} $$
B
$$\sqrt {\frac{{Gm}}{{3R}}} $$
C
$$\sqrt {\frac{{Gm}}{{2R}}} $$
D
$$\sqrt {\frac{{Gm}}{R}} $$
Answer :
$$\sqrt {\frac{{Gm}}{{4R}}} $$