31. Two spheres of masses $$m$$ and $$M$$ are situated in air and the gravitational force between them is $$F.$$ The space around the masses is now filled with a liquid of specific gravity $$3.$$ The gravitational force will now be
A
$$\frac{F}{9}$$
B
$$3F$$
C
$$F$$
D
$$\frac{F}{3}$$
Answer :
$$F$$
32. The escape velocity of a body depends upon mass as-
A
$${m^0}$$
B
$${m^1}$$
C
$${m^2}$$
D
$${m^3}$$
Answer :
$${m^0}$$
33.
This question contains Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best describes the two statements.
Statement-1 : For a mass $$M$$ kept at the centre of a cube of side $$'a\,',$$ the flux of gravitational field passing through its sides $$4\pi GM.$$
Statement-2 : If the direction of a field due to a point source is radial and its dependence on the distance $$'r\,'$$ from the source is given as $$\frac{1}{{{r^2}}},$$ its flux through a closed surface depends only on the strength of the source enclosed by the surface and not on the size or shape of the surface.
A
Statement -1 is false, Statement-2 is true
B
Statement -1 is true, Statement-2 is true; Statement -2 is a correct explanation for Statement-1
C
Statement -1 is true, Statement-2 is true; Statement -2 is not a correct explanation for Statement-1
D
Statement -1 is true, Statement-2 is false
Answer :
Statement -1 is true, Statement-2 is true; Statement -2 is a correct explanation for Statement-1
34. A spherical uniform planet is rotating about its axis. The velocity of a point on its equator is $$v.$$ Due to the rotation of planet about its axis the acceleration due to gravity $$g$$ at equator is $$\frac{1}{2}$$ of $$g$$ at poles. The escape velocity of a particle on the pole of planet in terms of $$v$$ is
A
$${v_e} = 2v$$
B
$${v_e} = v$$
C
$${v_e} = \frac{v}{2}$$
D
$${v_e} = \sqrt 3 v$$
Answer :
$${v_e} = 2v$$
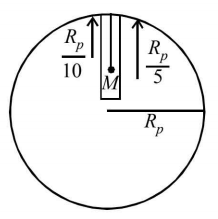
35. A planet of radius $$R = \frac{1}{{10}} \times \left( {{\text{radius of Earth}}} \right)$$ has the same mass density as Earth. Scientists dig a well of depth $$\frac{R}{5}$$ on it and lower a wire of the same length and a linear mass density $${10^{ - 3}}kg\,{m^{ - 1}}$$ into it. If the wire is not touching anywhere, the force applied at the top of the wire by a person holding it in place is (take the radius of Earth $$ = 6 \times {10^6}\,m$$ and the acceleration due to gravity on Earth is $$10\,m{s^{ - 2}}$$ )
A
$$94 \,N$$
B
$$108 \,N$$
C
$$120 \,N$$
D
$$150 \,N$$
Answer :
$$108 \,N$$
36. A satellite of mass $$m$$ is orbiting the earth in a circular orbit of radius $$R.$$ It starts losing energy due to small air resistance at the rate of $$C\,J/s.$$ Find the time taken for the satellite to reach the earth.
A
$$\frac{{GMm}}{C}\left[ {\frac{1}{R} - \frac{1}{r}} \right]$$
B
$$\frac{{GMm}}{{2C}}\left[ {\frac{1}{R} + \frac{1}{r}} \right]$$
C
$$\frac{{GMm}}{{2C}}\left[ {\frac{1}{R} - \frac{1}{r}} \right]$$
D
$$\frac{{2GMm}}{C}\left[ {\frac{1}{R} + \frac{1}{r}} \right]$$
Answer :
$$\frac{{GMm}}{{2C}}\left[ {\frac{1}{R} - \frac{1}{r}} \right]$$
37. If suddenly the gravitational force of attraction between Earth and a body revolving around it becomes zero, then the body will
A
continue to move in its orbit with same velocity
B
move tangentially to the original orbit with same velocity
C
become stationary in its orbit
D
move towards the earth
Answer :
move tangentially to the original orbit with same velocity
38. A particle of mass $$M$$ is situated at the centre of a spherical shell of same mass and radius $$a.$$ The gravitational potential at a point situated at $$\frac{a}{2}$$ distance from the centre, will be
A
$$ - \frac{{3GM}}{a}$$
B
$$ - \frac{{2GM}}{a}$$
C
$$ - \frac{{GM}}{a}$$
D
$$ - \frac{{4GM}}{a}$$
Answer :
$$ - \frac{{3GM}}{a}$$
39. A satellite $$A$$ of mass $$m$$ is at a distance of $$r$$ from the surface of the earth. Another satellite $$B$$ of mass $$2\,m$$ is at a distance of $$2\,r$$ from the earth’s centre. Their time periods are in the ratio of
A
$$1:2$$
B
$$1:16$$
C
$$1:32$$
D
$$1:2\sqrt 2 $$
Answer :
$$1:2\sqrt 2 $$
40. A remote sensing satellite of earth revolves in a circular orbit at a height of $$0.25 \times {10^6}m$$ above the surface of earth. If earth’s radius is $$6.38 \times {10^6}m$$ and $$g = 9.8\,m{s^{ - 2}},$$ then the orbital speed of the satellite is
A
$$7.76\,km{s^{ - 1}}$$
B
$$8.56\,km{s^{ - 1}}$$
C
$$9.13\,km{s^{ - 1}}$$
D
$$6.67\,km{s^{ - 1}}$$
Answer :
$$7.76\,km{s^{ - 1}}$$