11. A satellite $$A$$ of mass $$m$$ is at a distance $$r$$ from the surface of the earth. Another satellite $$B$$ of mass $$2\,m$$ is at a distance of $$2\,r$$ from the earth’s surface. Their time periods are in the ratio of
A
$$1:2$$
B
$$1:16$$
C
$$1:32$$
D
$$1:2\sqrt 2 $$
Answer :
$$1:2\sqrt 2 $$
12.
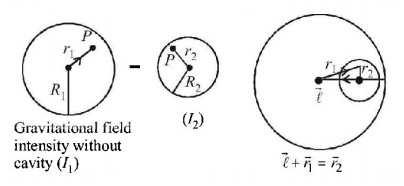
Inside a uniform sphere of density $$\rho $$ there is a spherical cavity whose centre is at a distance $$\ell $$ from the centre of the sphere. Find the strength $$F$$ of the gravitational field inside the cavity at the point $$P.$$

A
$$\frac{4}{3}G\pi \rho \vec \ell $$
B
$$\frac{1}{3}G\pi \rho \vec \ell $$
C
$$\frac{2}{3}G\pi \rho \vec \ell $$
D
$$\frac{1}{2}G\pi \rho \vec \ell $$
Answer :
$$\frac{4}{3}G\pi \rho \vec \ell $$
13. A simple pendulum is oscillating without damping. When the displacement of the bob is less than maximum, its acceleration vector $${\vec a}$$ is correctly shown in:
A
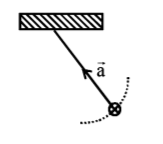

B
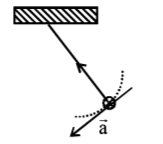

C
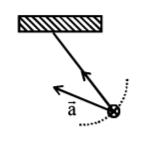

D
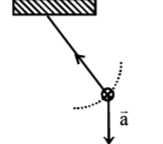

Answer :


14.
The gravitational field, due to the 'left over part’ of a uniform sphere (from which a part as shown, has been 'removed out’), at a very far off point, $$P,$$ located as shown, would be (nearly) :

A
$$\frac{5}{6}\frac{{GM}}{{{x^2}}}$$
B
$$\frac{8}{9}\frac{{GM}}{{{x^2}}}$$
C
$$\frac{7}{8}\frac{{GM}}{{{x^2}}}$$
D
$$\frac{6}{7}\frac{{GM}}{{{x^2}}}$$
Answer :
$$\frac{7}{8}\frac{{GM}}{{{x^2}}}$$
15. The radius of the earth is reduced by $$4\% .$$ The mass of the earth remains unchanged. What will be the change in escape velocity?
A
Increased by $$2\% $$
B
Decreased by $$4\% $$
C
Increased by $$6\% $$
D
Decreased by $$8\% $$
Answer :
Increased by $$2\% $$
16. Two spheres of masses $$m$$ and $$M$$ are situated in air and the gravitational force between them is $$F.$$ The space around the masses is now filled with a liquid of specific gravity 3. The gravitational force will now be
A
$$\frac{F}{3}$$
B
$$\frac{F}{9}$$
C
$$3F$$
D
$$F$$
Answer :
$$F$$
17. For a satellite moving in an orbit around the earth, the ratio of kinetic energy to potential energy is
A
$$2$$
B
$$\frac{1}{2}$$
C
$$\frac{1}{{\sqrt 2 }}$$
D
$$\sqrt 2 $$
Answer :
$$\frac{1}{2}$$
18. A rocket is launched normal to the surface of the Earth, away from the Sun, along the line joining the Sun and the Earth. The Sun is $$3 \times {10^5}$$ times heavier than the Earth and is at a distance $$2.5 \times {10^4}$$ times larger than the radius of the Earth. The escape velocity from Earth's gravitational field is $${v_e} = 11.2\,km\,{s^{ - 1}}.$$ The minimum initial velocity $$\left( {{v_s}} \right)$$ required for the rocket to be able to leave the Sun-Earth system is closest to (Ignore the rotation and revolution of the Earth and the presence of any other planet)-
A
$${v_s} = 22\,km\,{s^{ - 1}}$$
B
$${v_s} = 42\,km\,{s^{ - 1}}$$
C
$${v_s} = 62\,km\,{s^{ - 1}}$$
D
$${v_s} = 72\,km\,{s^{ - 1}}$$
Answer :
$${v_s} = 42\,km\,{s^{ - 1}}$$
19.
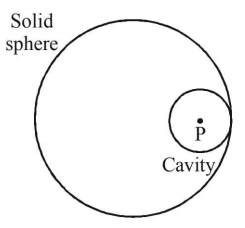
From a solid sphere of mass $$M$$ and radius $$R,$$ a spherical portion of radius $$\frac{R}{2}$$ is removed, as shown in the figure. Taking gravitational potential $$V=0$$ at $$r = \infty ,$$ the potential at the centre of the cavity thus formed is-
($$G\,=$$ gravitational constant)
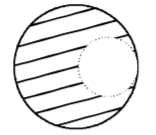
A
$$\frac{{ - 2GM}}{{3R}}$$
B
$$\frac{{ - 2GM}}{{R}}$$
C
$$\frac{{ - GM}}{{2R}}$$
D
$$\frac{{ - GM}}{{R}}$$
Answer :
$$\frac{{ - GM}}{{R}}$$
20. If the radius of the earth were to shrink by one percent, its mass remaining the same, the acceleration due to gravity on the earth’s surface would-
A
Decrease
B
Remain unchanged
C
Increase
D
Be zero
Answer :
Increase