Question
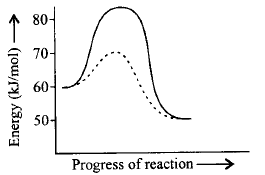
For a reaction, $${A_2} + {B_2} \rightleftharpoons 2AB$$ the figure shows the path of the reaction in absence and presence of a catalyst. What will be the energy of activation for forward $$\left( {{E_f}} \right)$$ and backward $$\left( {{E_b}} \right)$$ reaction in presence of a catalyst and $$\Delta H$$ for the reaction? The dotted curve is the path of reaction in presence of a catalyst.
For a reaction, $${A_2} + {B_2} \rightleftharpoons 2AB$$ the figure shows the path of the reaction in absence and presence of a catalyst. What will be the energy of activation for forward $$\left( {{E_f}} \right)$$ and backward $$\left( {{E_b}} \right)$$ reaction in presence of a catalyst and $$\Delta H$$ for the reaction? The dotted curve is the path of reaction in presence of a catalyst.
A.
$${E_f} = 60\,kJ/mol,{E_b} = 70\,kJ/mol,$$ $$\Delta H = 20\,kJ/mol$$
B.
$${E_f} = 20\,kJ/mol,{E_b} = 20\,kJ/mol,$$ $$\Delta H = 50\,kJ/mol$$
C.
$${E_f} = 70\,kJ/mol,{E_b} = 20\,kJ/mol,$$ $$\Delta H = 10\,kJ/mol$$
D.
$${E_f} = 10\,kJ/mol,{E_b} = 20\,kJ/mol,$$ $$\Delta H = - 10\,kJ/mol$$
Answer :
$${E_f} = 10\,kJ/mol,{E_b} = 20\,kJ/mol,$$ $$\Delta H = - 10\,kJ/mol$$
Solution :
$$\eqalign{ & {E_f} = 70 - 60 = 10\,kJ/mol \cr & {E_b} = 70 - 50 = 20\,kJ/mol \cr & \Delta H = 50 - 60 = - 10\,kJ/mol \cr} $$
$$\eqalign{ & {E_f} = 70 - 60 = 10\,kJ/mol \cr & {E_b} = 70 - 50 = 20\,kJ/mol \cr & \Delta H = 50 - 60 = - 10\,kJ/mol \cr} $$