221. For the exothermic reaction $$A + B \to C + D,\Delta H$$ is the heat of reaction and $${E_a}$$ is the energy of activation. The energy of activation for the formation of $$A + B$$ will be
A
$${E_a}$$
B
$$\Delta H$$
C
$${E_a} + \Delta H$$
D
$$\Delta H - {E_a}$$
Answer :
$${E_a} + \Delta H$$
222.
Rate constant of two reactions are given below. Identify their order of reaction.
$$\eqalign{
& \left( {\text{i}} \right)k = 5.3 \times {10^{ - 2}}\,L\,mo{l^{ - 1}}\,{s^{ - 1}} \cr
& \left( {{\text{ii}}} \right)k = 3.8 \times {10^{ - 4}}\,{s^{ - 1}} \cr} $$
A
(i) second order, (ii) first order
B
(i) first order, (ii) second order
C
(i) zero order, (ii) first order
D
(i) second order, (ii) zero order
Answer :
(i) second order, (ii) first order
223. When a biochemical reaction is carried out in laboratory from outside of human body in the absence of enzyme, the rate of reaction obtained is $${10^{ - 6}}$$ times, then activation energy of the reaction in the presence of enzyme is
A
$$\frac{6}{{RT}}$$
B
$$P$$ is required
C
different from $${E_a}$$ obtained in laboratory
D
cannot say any things
Answer :
different from $${E_a}$$ obtained in laboratory
224. For a first order reaction $$(A) →$$ products the concentration of A changes from $$0.1 M$$ to $$0.025 M$$ in 40 minutes. The rate of reaction when the concentration of $$A$$ is $$0.01 M$$ is :
A
$$1.73 \times {10^{ - 5}}M/\min $$
B
$$3.47 \times {10^{ - 4}}M/\min $$
C
$$3.47 \times {10^{ - 5}}M/\min $$
D
$$1.73 \times {10^{ - 4}}M/\min $$
Answer :
$$3.47 \times {10^{ - 4}}M/\min $$
225.
Mechanism of a hypothetical reaction $${X_2} + {Y_2} \to 2XY$$ is given below
$$\eqalign{
& \left( {\text{i}} \right){X_2} \rightleftharpoons X + X\left( {{\text{fast}}} \right) \cr
& \left( {{\text{ii}}} \right)X + {Y_2} \to XY + Y\left( {{\text{slow}}} \right) \cr
& \left( {{\text{iii}}} \right)X + Y \to XY\,\left( {{\text{fast}}} \right) \cr} $$
The overall order of the reaction will be
A
1
B
2
C
0
D
1.5
Answer :
1.5
226. A first order reaction has a specific reaction rate of $${10^{ - 2}}{s^{ - 1}}.$$ How much time will it take for $$20$$ $$g$$ of the reactant to reduce to $$5$$ $$g?$$
A
238.6$$\,s$$
B
138.6$$\,s$$
C
346.5$$\,s$$
D
693.0$$\,s$$
Answer :
138.6$$\,s$$
227. Which one of the following statements for the order of a reaction is incorrect?
A
Order is not influenced by stoichiometric coefficient of the reactants
B
Order of reaction is sum of power to the concentration terms of reactants to express the rate of reaction
C
Order of reaction is always whole number
D
Order can be determined only experimentally
Answer :
Order of reaction is always whole number
228. A first order reaction is $$50\% $$ complete in 30 minutes at $${27^ \circ }C$$ and in 10 minutes at $${47^ \circ }C.$$ The reaction rate constant at $${27^ \circ }C$$ and the energy of activation of the reaction are respectively
A
\[k=0.0231\,{{\min }^{-1}},\] $${E_a} = 43.848\,kJ\,mo{l^{ - 1}}$$
B
\[k=0.017\,{{\min }^{-1}},\] $${E_a} = 52.54\,kJ\,mo{l^{ - 1}}$$
C
\[k=0.0693\,{{\min }^{-1}},\] $${E_a} = 43.848\,kJ\,mo{l^{ - 1}}$$
D
\[k=0.0231\,{{\min }^{-1}},\] $${E_a} = 28.92\,kJ\,mo{l^{ - 1}}$$
Answer :
\[k=0.0231\,{{\min }^{-1}},\] $${E_a} = 43.848\,kJ\,mo{l^{ - 1}}$$
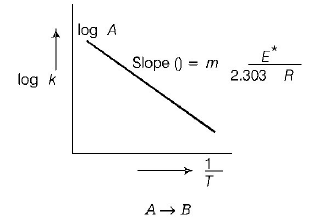
229. The temperature dependence of rate constant $$\left( k \right)$$ of a chemical reaction is written in terms of Arrhenius equation, $$k = A{e^{ - \,\frac{{{E^*}}}{{RT}}}}.$$ Activation energy $$\left( {{E^*}} \right)$$ of the reaction can be calculated by plotting
A
$${\text{log}}\,k\,\,{\text{vs}}\,\,\frac{1}{T}$$
B
$${\text{log}}\,k\,\,{\text{vs}}\,\,\frac{1}{{{\text{log}}\,T}}$$
C
$$k\,\,{\text{vs}}\,\,T$$
D
$$k\,\,{\text{vs}}\,\,\frac{1}{{\log \,T}}$$
Answer :
$${\text{log}}\,k\,\,{\text{vs}}\,\,\frac{1}{T}$$
230. The reaction, $$A$$ → Product, follows first order kinetics. In 40 minutes the concentration of $$A$$ changes from $$0.1$$ to $$0.025 M.$$ The rate of reaction, when concentration of $$A$$ is $$0.01 M$$ is
A
B
C
D
Answer :