161.
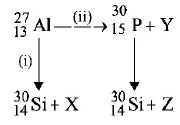
Bombardment of aluminium by $$o-$$ particle leads to its artificial disintegration in two ways, (i) and (ii) as shown. Products $$X, Y$$ and $$Z$$ respectively are,
A
proton, neutron, positron
B
neutron, positron, proton
C
proton, positron, neutron
D
positron, proton, neutron
Answer :
proton, neutron, positron
162. In the presence of a catalyst, the heat evolved or absorbed during the reaction _________.
A
increases
B
decreases
C
remains unchanged
D
may increase or decrease
Answer :
remains unchanged
163.
Two reactions $${R_1}$$ and $${R_2}$$ have identical pre-exponential factors. Activation energy of $${R_1}$$ exceeds that of $${R_2}$$ by $$10\,kJ\,mo{l^{ - 1}}.$$ If $${k_1}$$ and $${k_2}$$ are rate constants for reactions $${R_1}$$ and $${R_2}$$ respectively at $$300 K$$ , then In $$\left( {{k_2}/{k_1}} \right)$$ is equal to :
$$\left( {R = 8.314\,J\,mo{l^{ - 1}}{K^{ - 1}}} \right)$$
A
8
B
12
C
6
D
4
Answer :
4
164.
Rate of a reaction can be expressed by Arrhenius equation as : $$k = A{e^{ - \,\frac{E}{{RT}}}}$$
In this equation, $$E$$ represents
A
the total energy of the reacting molecules at a temperature, $$T$$
B
the fraction of molecules with energy greater than the activation energy of the reaction
C
the energy above which all the colliding molecules will react
D
the energy below which all the colliding molecules will react
Answer :
the energy above which all the colliding molecules will react
165.
Consider the reaction :
$$C{l_2}\left( {aq} \right) + {H_2}S\left( {aq} \right) \to $$ $$S\left( s \right) + 2{H^ + }\left( {aq} \right) + 2C{l^ - }\left( {aq} \right)$$
The rate equation for this reaction is
rate $$ = k\left[ {C{l_2}} \right]\left[ {{H_2}S} \right]$$
Which of these mechanisms is/are consistent with this rate equation?
$${\text{A}}{\text{.}}\,\,C{l_2} + {H_2}S \to {H^ + } + C{l^ - } + C{l^ + }$$ $$ + H{S^ - }\left( {{\text{slow}}} \right)$$
$$C{l^ + } + H{S^ - } \to {H^ + } + C{l^ - } + S\left( {{\text{fast}}} \right)$$
$${\text{B}}{\text{.}}\,\,{H_2}S \rightleftharpoons {H^ + } + H{S^ - }$$ $$\left( {{\text{fast equilibrium}}} \right)$$
$$C{l_2} + H{S^ - } \to 2C{l^ - } + {H^ + } + S\left( {{\text{slow}}} \right)$$
A
B only
B
Both A and B
C
Neither A nor B
D
A only
Answer :
A only
166. For a reaction, activation energy $$\left( {{E_a}} \right) = 0$$ and rate constant $$\left( k \right) = 3.2 \times {10^6}{s^{ - 1}}$$ at $$300\,K.$$ What is the value of the rate constant at $$310\,K$$
A
$$3.2 \times {10^{ - 12}}{s^{ - 1}}$$
B
$$3.2 \times {10^6}{s^{ - 1}}$$
C
$$6.4 \times {10^{12}}{s^{ - 1}}$$
D
$$6.4 \times {10^6}{s^{ - 1}}$$
Answer :
$$3.2 \times {10^6}{s^{ - 1}}$$
167. In a first order reaction, $$A \to B,$$ if $$k$$ is rate constant and initial concentration of the reactant $$A$$ is $$0.5$$ $$M,$$ then the half-life is
A
$$\frac{{0.693}}{{0.5k}}$$
B
$$\frac{{{\text{log}}\,2}}{k}$$
C
$$\frac{{{\text{log}}2}}{{k\sqrt {0.5} }}$$
D
$$\frac{{{\text{ln}}\,2}}{k}$$
Answer :
$$\frac{{{\text{ln}}\,2}}{k}$$
168. The activation energies of the forward and backward reactions in the case of a chemical reaction are $$30.5$$ and $$45.4\,kJ/mol$$ respectively. The reaction is :
A
exothermic
B
endothermic
C
neither exothermic nor endothermic
D
independent of temperature
Answer :
exothermic
169.
The decomposition of dinitrogen pentoxide $$\left( {{N_2}{O_5}} \right)$$ follows first order rate law. What will be the rate constant from the given data?
$$\eqalign{
& {\text{At}}\,t = 800\,s{\text{,}}\left[ {{N_2}{O_5}} \right] = 1.45\,mol\,{L^{ - 1}} \cr
& {\text{At}}\,t = 1600\,s,\left[ {{N_2}{O_5}} \right] = 0.88\,mol\,{L^{ - 1}} \cr} $$
A
$$3.12 \times {10^{ - 4}}\,{s^{ - 1}}$$
B
$$6.24 \times {10^{ - 4}}\,{s^{ - 1}}$$
C
$$2.84 \times {10^{ - 4}}\,{s^{ - 1}}$$
D
$$8.14 \times {10^{ - 4}}\,{s^{ - 1}}$$
Answer :
$$6.24 \times {10^{ - 4}}\,{s^{ - 1}}$$
170.
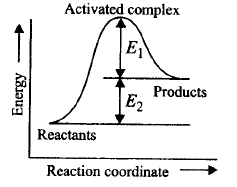
Consider figure and mark the correct option.
A
Activation energy of forward reaction is $${E_1} + {E_2}$$ and product is less stable than reactant.
B
Activation energy of forward reaction is $${E_1} + {E_2}$$ and product is more stable than reactant.
C
Activation energy of both forward and backward reaction is $${E_1} + {E_2}$$ and reactant is more stable than product.
D
Activation energy of backward reaction is $${E_1}$$ and product is more stable than reactant.
Answer :
Activation energy of forward reaction is $${E_1} + {E_2}$$ and product is less stable than reactant.