Question
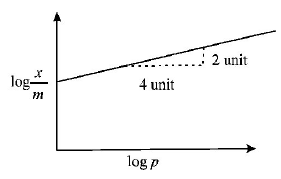
Adsorption of a gas follows Freundlich adsorption isotherm. In the given plot, $$x$$ is the mass of the gas adsorbed on mass m of the adsorbent at pressure $$p.$$ $$\frac{x}{m}$$ is proportional to :
Adsorption of a gas follows Freundlich adsorption isotherm. In the given plot, $$x$$ is the mass of the gas adsorbed on mass m of the adsorbent at pressure $$p.$$ $$\frac{x}{m}$$ is proportional to :
A.
$${p^2}$$
B.
$${p^{\frac{1}{4}}}$$
C.
$${p^{\frac{1}{2}}}$$
D.
$$p$$
Answer :
$${p^{\frac{1}{2}}}$$
Solution :
In Freundlich adsorption isotherm the extent of adsorption $$\left( {\frac{x}{m}} \right)$$ of a gas on the surface of a solid is related to the pressure of the gas $$(P)$$ which can be formulated as :
$$\eqalign{ & \frac{x}{m} = k{\left( p \right)^{\frac{1}{n}}} \cr & \Rightarrow \,\log \,\frac{x}{m} = \log k + \frac{1}{n}\,\log p \cr} $$
In the given plot, the slope between $$\log \,\frac{x}{m}$$ versus
$$\eqalign{ & \log \,p = \frac{2}{4} = \frac{1}{2} \cr & \therefore \,\,\frac{x}{m} \propto {p^{\frac{1}{2}}} \cr} $$
In Freundlich adsorption isotherm the extent of adsorption $$\left( {\frac{x}{m}} \right)$$ of a gas on the surface of a solid is related to the pressure of the gas $$(P)$$ which can be formulated as :
$$\eqalign{ & \frac{x}{m} = k{\left( p \right)^{\frac{1}{n}}} \cr & \Rightarrow \,\log \,\frac{x}{m} = \log k + \frac{1}{n}\,\log p \cr} $$
In the given plot, the slope between $$\log \,\frac{x}{m}$$ versus
$$\eqalign{ & \log \,p = \frac{2}{4} = \frac{1}{2} \cr & \therefore \,\,\frac{x}{m} \propto {p^{\frac{1}{2}}} \cr} $$