Question
A reaction rate constant is given by $$k = 1.2 \times {10^{14}}{e^{ - \frac{{25000}}{{RT}}}}{\sec ^{ - 1}}.$$ It means
A.
$${\text{log}}\,k$$ versus $${\text{log}}\,T$$ will give a straight line with a slope as - 25000
B.
$${\text{log}}\,k$$ versus $$T$$ will give a straight line with slope as 25000
C.
$${\text{log}}\,k$$ versus $$\frac{1}{T}$$ will give a straight line with slope as $$ - \frac{{25000}}{R}$$
D.
$${\text{log}}\,k$$ versus $$\frac{1}{T}$$ will give a straight line
Answer :
$${\text{log}}\,k$$ versus $$\frac{1}{T}$$ will give a straight line with slope as $$ - \frac{{25000}}{R}$$
Solution :
$$\eqalign{ & k = 1.2 \times {10^{14}}{e^{ - \frac{{25000}}{{RT}}}}{\sec ^{ - 1}}\,\,{\text{or}} \cr & {\text{log}}\,k = {\text{log}}\,1.2 \times {10^{14}} - \frac{{25000}}{R}.\frac{1}{T} \cr} $$
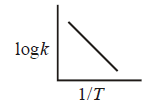
$$\eqalign{ & {\text{Equation of straight line}} \cr & {\text{slope}} = - \frac{{25000}}{R} \cr} $$
$$\eqalign{ & k = 1.2 \times {10^{14}}{e^{ - \frac{{25000}}{{RT}}}}{\sec ^{ - 1}}\,\,{\text{or}} \cr & {\text{log}}\,k = {\text{log}}\,1.2 \times {10^{14}} - \frac{{25000}}{R}.\frac{1}{T} \cr} $$
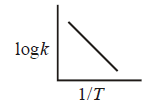
$$\eqalign{ & {\text{Equation of straight line}} \cr & {\text{slope}} = - \frac{{25000}}{R} \cr} $$