Question
A given mass of gas expands from state $$A$$ to state $$B$$ by three paths 1, 2, and 3 as shown in the figure :
A given mass of gas expands from state $$A$$ to state $$B$$ by three paths 1, 2, and 3 as shown in the figure :
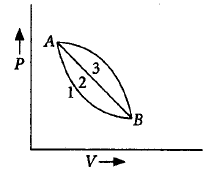
If $${w_1},{w_2}$$ and $${w_3}$$ respectively, be the work done by the gas along three paths, then
A.
$${w_1} > {w_2} > {w_3}$$
B.
$${w_1} < {w_2} < {w_3}$$
C.
$${w_1} = {w_2} = {w_3}$$
D.
$${w_2} > {w_1} > {w_3}$$
Answer :
$${w_1} < {w_2} < {w_3}$$
Solution :
Work is equal to area under $$P - V$$ graph ( when $$P$$ is plotted along $$y$$ - axis ). As area under graph 3 is maximum and area under graph 1 is minimum, so $${w_3}$$ is minimum and $${w_1}$$ is minimum.
$$\therefore \,\,{w_1} < {w_2} < {w_3}$$

Work is equal to area under $$P - V$$ graph ( when $$P$$ is plotted along $$y$$ - axis ). As area under graph 3 is maximum and area under graph 1 is minimum, so $${w_3}$$ is minimum and $${w_1}$$ is minimum.
$$\therefore \,\,{w_1} < {w_2} < {w_3}$$
