111. A point object $$'O'$$ is at the centre of curvature of a concave mirror. The mirror starts to move at a speed $$u,$$ in a direction perpendicular to the principal axis. Then, the initial velocity of the image is
A
$$2u,$$ in the direction opposite to that of mirror's velocity
B
$$2u,$$ in the direction same as that of mirror's velocity
C
zero
D
$$u,$$ in the direction same as that of mirror's velocity
Answer :
$$2u,$$ in the direction same as that of mirror's velocity
112. A boy is trying to start a fire by focusing sunlight on a piece of paper using an equiconvex lens of focal length $$10\,cm.$$ The diameter of the sun is $$1.39 \times {10^9}m$$ and its mean distance from the earth is $$1.5 \times {10^{11}}m.$$ What is the diameter of the sun’s image on the paper ?
A
$$9.2 \times {10^{ - 4}}m$$
B
$$6.5 \times {10^{ - 4}}m$$
C
$$6.5 \times {10^{ - 5}}m$$
D
$$12.4 \times {10^{ - 4}}m$$
Answer :
$$9.2 \times {10^{ - 4}}m$$
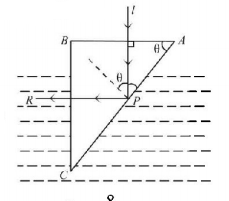
113.
A glass prism of refractive index $$1.5$$ is immersed in water (refractive index $$\frac{4}{3}$$ ). A light beam incident normally on the face $$AB$$ is totally reflected to reach on the face $$BC$$ if
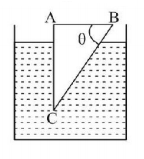
A
$$\sin \theta \geqslant \frac{8}{9}$$
B
$$\frac{2}{3} < \sin \theta < \frac{8}{9}$$
C
$$\sin \theta \leqslant \frac{2}{3}$$
D
$$\frac{1}{2} < \sin \theta < 1$$
Answer :
$$\sin \theta \geqslant \frac{8}{9}$$
114. A biconvex lens has a radius of curvature of magnitude $$20\,cm.$$ Which one of the following options describe best the image formed of an object of height $$2\,cm$$ placed $$30\,cm$$ from the lens?
A
Virtual, upright, height $$= 0.5\,cm$$
B
Real, inverted, height $$= 4\,cm$$
C
Real, inverted, height $$= 1\,cm$$
D
Virtual, upright, height $$= 1\,cm$$
Answer :
Real, inverted, height $$= 4\,cm$$
115. An experiment is performed to find the refractive index of glass using a travelling microscope. In this experiment distances are measured by
A
a vernier scale provided on the microscope
B
a standard laboratory scale
C
a meter scale provided on the microscope
D
a screw gauge provided on the microscope
Answer :
a vernier scale provided on the microscope
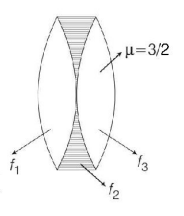
116. Two identical glass $$\left( {{\mu _g} = \frac{3}{2}} \right)$$ equi-convex lenses of focal length $$f$$ each are kept in contact. The space between the two lenses is filled with water $$\left( {{\mu _w} = \frac{4}{3}} \right).$$ The focal length of the combination is
A
$$\frac{f}{3}$$
B
$$f$$
C
$$\frac{{4f}}{3}$$
D
$$\frac{{3f}}{4}$$
Answer :
$$\frac{{3f}}{4}$$
117.
In figure find the total magnification after two successive reflections first on $${M_1}$$ and then on $${M_2}.$$
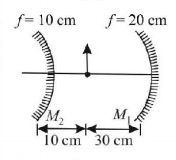
A
$$+ 1$$
B
$$- 2$$
C
$$+ 2$$
D
$$- 1$$
Answer :
$$+ 2$$
118. Light with an energy flux of $$25 \times {10^4}\,W{m^{ - 2}}$$ falls on a perfectly reflecting surface at normal incidence. If the surface area is $$15\,c{m^2},$$ the average force exerted on the surface is
A
$$1.25 \times {10^{ - 6}}N$$
B
$$2.50 \times {10^{ - 6}}N$$
C
$$1.20 \times {10^{ - 6}}N$$
D
$$3.0 \times {10^{ - 6}}N$$
Answer :
$$2.50 \times {10^{ - 6}}N$$
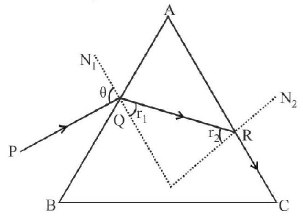
119.
Monochromatic light is incident on a glass prism of angle $$A.$$ If the refractive index of the material of the prism is $$\mu ,$$ $$a$$ ray, incident at an angle $$\theta ,$$ on the face $$AB$$ would get transmitted through the face $$AC$$ of the prism provided :

A
$$\theta > {\cos ^{ - 1}}\left[ {\mu \sin \left( {A + {{\sin }^{ - 1}}\left( {\frac{1}{\mu }} \right)} \right.} \right]$$
B
$$\theta < {\cos ^{ - 1}}\left[ {\mu \sin \left( {A + {{\sin }^{ - 1}}\left( {\frac{1}{\mu }} \right)} \right.} \right]$$
C
$$\theta > {\sin ^{ - 1}}\left[ {\mu \sin \left( {A - {{\sin }^{ - 1}}\left( {\frac{1}{\mu }} \right)} \right.} \right]$$
D
$$\theta < {\sin ^{ - 1}}\left[ {\mu \sin \left( {A - {{\sin }^{ - 1}}\left( {\frac{1}{\mu }} \right)} \right.} \right]$$
Answer :
$$\theta > {\sin ^{ - 1}}\left[ {\mu \sin \left( {A - {{\sin }^{ - 1}}\left( {\frac{1}{\mu }} \right)} \right.} \right]$$
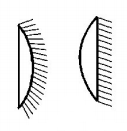
120. Two identical thin plano convex lenses of refractive index $$n$$ are silvered, one on the plane side and the other on the convex side. The ratio of their focal lengths is
A
$$\frac{n}{{n - 1}}$$
B
$$\frac{{n - 1}}{n}$$
C
$$\frac{{n + 1}}{n}$$
D
$$n$$
Answer :
$$\frac{n}{{n - 1}}$$