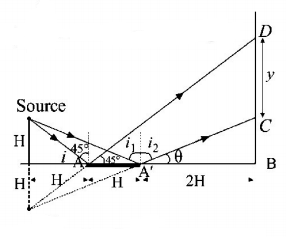
101.
A point source has been placed as shown in the figure. What is the length on the screen that will receive reflected light from the mirror?

A
$$2\,H$$
B
$$3\,H$$
C
$$H$$
D
None of these
Answer :
$$2\,H$$
102. A person can see clearly objects only when they lie between $$50\,cm$$ and $$400\,cm$$ from his eyes. In order to increase the maximum distance of distinct vision to infinity, the type and power of the correcting lens, the person has to use, will be
A
convex, + 2.25 diopter
B
concave, - 0.25 diopter
C
concave - 0.2 diopter
D
convex, + 0.15 diopter
Answer :
concave, - 0.25 diopter
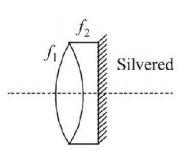
103.
Two lenses of focal length $${f_1} = 10\,cm$$ and $${f_2} = - 20\,cm$$ are kept as shown. The resultant power of combination will be
A
$$-10\,D$$
B
$$5\,D$$
C
0
D
$$10\,D$$
Answer :
$$10\,D$$
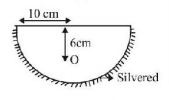
104.
A hemispherical glass body of radius $$10\,cm$$ and refractive index $$1.5$$ is silvered on its curved surface. A small air bubble is $$6\,cm$$ below the flat surface inside it along the axis. The position of the image of the air bubble made by the mirror is seen :
A
$$14\,cm$$ below flat surface
B
$$20\,cm$$ below flat surface
C
$$16\,cm$$ below flat surface
D
$$30\,cm$$ below flat surface
Answer :
$$20\,cm$$ below flat surface
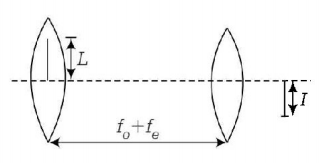
105. In an astronomical telescope in normal adjustment a straight black line of length $$L$$ is drawn on inside part of objective lens. The eye-piece forms a real image of this line. The length of this image is $$I.$$ The magnification of the telescope is
A
$$\frac{L}{I} + 1$$
B
$$\frac{L}{I} - 1$$
C
$$\frac{{L + 1}}{{L - 1}}$$
D
$$\frac{L}{I}$$
Answer :
$$\frac{L}{I}$$
106.
A light ray is incident perpendicularly to one face of a 90° prism and is totally internally reflected at the glass - air interface. If the angle of reflection is 45°, we conclude that the refractive index $$n$$
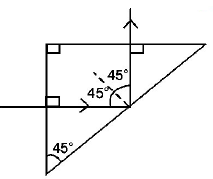
A
$$n > \frac{1}{{\sqrt 2 }}$$
B
$$n > \sqrt 2 $$
C
$$n < \frac{1}{{\sqrt 2 }}$$
D
$$n < \sqrt 2 $$
Answer :
$$n > \sqrt 2 $$
107.
An equiconvex lens is cut into two halves along (i) $$XOX'$$ and (ii) $$YOY'$$ as shown in the figure. Let $$f,f',f''$$ be the focal lengths of the complete lens, of each half in case (i), and of each half in case (ii), respectively.
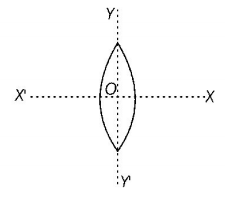
Choose the correct statement from the following
A
$$f' = f,f'' = f$$
B
$$f' = 2f,f'' = 2f$$
C
$$f' = f,f'' = 2f$$
D
$$f' = 2f,f'' = f$$
Answer :
$$f' = f,f'' = 2f$$
108. A plano convex lens of refractive index 1.5 and radius of curvature $$30\,cm.$$ Is silvered at the curved surface. Now this lens has been used to form the image of an object. At what distance from this lens an object be placed in order to have a real image of size of the object
A
$$60\,cm$$
B
$$30\,cm$$
C
$$20\,cm$$
D
$$80\,cm$$
Answer :
$$20\,cm$$
109. Two point white dots are $$1\,mm$$ apart on a black paper. They are viewed by eye of pupil diameter $$3\,mm.$$ Approximately, what is the maximum distance at which these dots can be resolved by the eye? [Take wavelength of light = $$500\,nm$$ ]
A
$$1\,m$$
B
$$5\,m$$
C
$$3\,m$$
D
$$6\,m$$
Answer :
$$5\,m$$
110. A point object $$P$$ moves towards a stationary convex mirror with a constant speed $$v,$$ along the optical axis. The speed of the image
A
is always less than $$v$$
B
maybe greater than, equal to or less than $$v,$$ depending upon the position of $$P$$
C
is always greater than $$v$$
D
None of these
Answer :
is always less than $$v$$