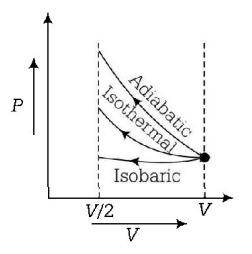
181. An ideal gas is compressed to half its initial volume by means of several process. Which of the process results in the maximum work done on the gas?
A
Adiabatic
B
Isobaric
C
lsochoric
D
Isothermal
Answer :
Adiabatic
182. An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume $${V_1}$$ and contains ideal gas at pressure $${P_1}$$ and temperature $${T_1}.$$ The other chamber has volume $${V_2}$$ and contains ideal gas at pressure $${P_2}$$ and temperature $${T_2}.$$ If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
A
$$\frac{{{T_1}{T_2}\left( {{P_1}{V_1} + {P_2}{V_2}} \right)}}{{{P_1}{V_1}{T_2} + {P_2}{V_2}{T_1}}}$$
B
$$\frac{{{P_1}{V_1}{T_1} + {P_2}{V_2}{T_2}}}{{{P_1}{V_1} + {P_2}{V_2}}}$$
C
$$\frac{{{P_1}{V_1}{T_2} + {P_2}{V_2}{T_1}}}{{{P_1}{V_1} + {P_2}{V_2}}}$$
D
$$\frac{{{T_1}{T_2}\left( {{P_1}{V_1} + {P_2}{V_2}} \right)}}{{{P_1}{V_1}{T_1} + {P_2}{V_2}{T_2}}}$$
Answer :
$$\frac{{{T_1}{T_2}\left( {{P_1}{V_1} + {P_2}{V_2}} \right)}}{{{P_1}{V_1}{T_2} + {P_2}{V_2}{T_1}}}$$
183.
An ideal gas has temperature $${T_1}$$ at the initial state i shown in the $$P-V$$ diagram. The gas has a higher temperature $${T_2}$$ at the final states $$a$$ and $$b,$$ which it can reach the paths shown. The change in entropy:
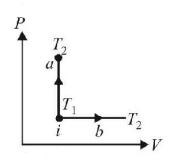
A
greatest in $$a$$
B
greatest in $$b$$
C
same in $$a$$ and $$b$$
D
nothing can be said
Answer :
greatest in $$b$$
184. An ideal gas undergoing adiabatic change has the following pressure-temperature relationship
A
$${p^{\gamma - 1}}{T^\gamma } = {\text{constant}}$$
B
$${p^\gamma }{T^{\gamma - 1}} = {\text{constant}}$$
C
$${p^\gamma }{T^{1 - \gamma }} = {\text{constant}}$$
D
$${p^{1 - \gamma }}{T^\gamma } = {\text{constant}}$$
Answer :
$${p^{1 - \gamma }}{T^\gamma } = {\text{constant}}$$
185. The slopes of isothermal and adiabatic curves are related as
A
isothermal curve slope $$=$$ adiabatic curve slope
B
isothermal curve slope $$ = \gamma \times $$ adiabatic curve slope
C
adiabatic curve slope $$ = \gamma \times $$ isothermal curve slope
D
adiabatic curve slope $$ = \frac{1}{2} \times $$ isothermal curve slope
Answer :
adiabatic curve slope $$ = \gamma \times $$ isothermal curve slope
186. During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its temperature. The ratio of $$\frac{{{C_P}}}{{{C_V}}}$$ for the gas is
A
$$\frac{4}{3}$$
B
$$2$$
C
$$\frac{5}{3}$$
D
$$\frac{3}{2}$$
Answer :
$$\frac{3}{2}$$
187. A diatomic ideal gas is used in a car engine as the working substance. If during the adiabatic expansion part of the cycle, volume of the gas increases from $$V$$ to $$32\,V,$$ the efficiency of the engine is
A
0.5
B
0.75
C
0.99
D
0.25
Answer :
0.75
188. An ideal gas heat engine operates in Carnot cycle between $${227^ \circ }C$$ and $${127^ \circ }C.$$ It absorbs $$6 \times {10^4}cal$$ of heat at higher temperature. Amount of heat converted to work is
A
$$2.4 \times {10^4}cal$$
B
$$6 \times {10^4}cal$$
C
$$1.2 \times {10^4}cal$$
D
$$4.8 \times {10^4}cal$$
Answer :
$$1.2 \times {10^4}cal$$
189. What will be the final pressure if an ideal gas in a cylinder is compressed adiabatically to $$\frac{1}{3}rd$$ of its volume?
A
Final pressure will be three times less than initial pressure.
B
Final pressure will be three times more than initial pressure.
C
Change in pressure will be more than three times the initial pressure.
D
Change in pressure will be less than three times the initial pressure.
Answer :
Change in pressure will be more than three times the initial pressure.
190. $$1\,gm$$ of water at a pressure of $$1.01 \times {10^5}\,Pa$$ is converted into steam without any change of temperature. The volume of $$1\,g$$ of steam is $$1671\,cc$$ and the latent heat of evaporation is $$540\,cal.$$ The change in internal energy due to evaporation of $$1\,gm$$ of water is
A
$$ \approx 167\,cal$$
B
$$ \approx 500\,cal$$
C
$$540\,cal$$
D
$$581\,cal$$
Answer :
$$ \approx 500\,cal$$