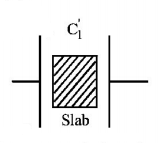
61. A sheet of aluminium foil of negligible thickness is introduced between the plates of a capacitor. The capacitance of the capacitor
A
decreases
B
remains unchanged
C
becomes infinite
D
increases
Answer :
remains unchanged
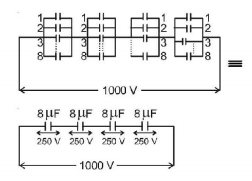
62. A capacitance of $$2\mu F$$ is required in an electrical circuit across a potential difference of $$1.0 kV.$$ A large number of $$1\mu F$$ capacitors are available which can withstand a potential difference of not more than $$300 V.$$ The minimum number of capacitors required to achieve this is
A
24
B
32
C
2
D
16
Answer :
32
63.
Two condensers, one of capacity $$C$$ and the other of capacity $$\frac{C}{2},$$ are connected to a $$V$$ volt battery, as shown.
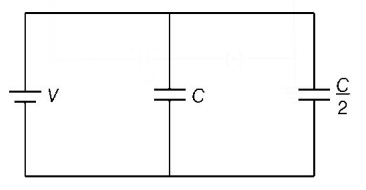
The work done in charging fully both the condensers is
A
$$2C{V^2}$$
B
$$\frac{1}{4}C{V^2}$$
C
$$\frac{3}{4}C{V^2}$$
D
$$\frac{1}{2}C{V^2}$$
Answer :
$$\frac{3}{4}C{V^2}$$
64. Capacitance (in $$F$$ ) of a spherical conductor with radius $$1\,m$$ is
A
$$1.1 \times {10^{ - 10}}$$
B
$${10^6}$$
C
$$9 \times {10^{ - 9}}$$
D
$${10^{ - 3}}$$
Answer :
$$1.1 \times {10^{ - 10}}$$
65. A parallel plate air capacitor of capacitance $$C$$ is connected to a cell of emf $$V$$ and then disconnected from it. A dielectric slab of dielectric constant $$K,$$ which can just fill the air gap of the capacitor, is now inserted in it. Which of the following is incorrect?
A
The potential difference between the plates decreases $$K$$ times
B
The energy stored in the capacitor decreases $$K$$ times
C
The change in energy stored is $$\frac{1}{2}C{V^2}\left( {\frac{1}{K} - 1} \right)$$
D
The charge on the capacitor is not conserved
Answer :
The charge on the capacitor is not conserved
66.
A combination of parallel plate capacitors is maintained at a certain potential difference.
When a $$3\,mm$$ thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between the plates is increased by $$2.4\,mm.$$
Find the dielectric constant of the slab.
A
3
B
4
C
5
D
6
Answer :
5
67. A series combination of $${n_1}$$ capacitors, each of value $${C_1},$$ is charged by a source of potential difference $$4V.$$ When another parallel combination of $${n_2}$$ capacitors, each of value $${C_2},$$ is charged by a source of potential difference $$V,$$ it has the same (total) energy stored in it, as the first combination has. The value of $${C_2},$$ in terms of $${C_1},$$ is then
A
$$\frac{{2{C_1}}}{{{n_1}{n_2}}}$$
B
$$16\frac{{{n_2}}}{{{n_1}}}{C_1}$$
C
$$2\frac{{{n_2}}}{{{n_1}}}{C_1}$$
D
$$\frac{{16{C_1}}}{{{n_1}{n_2}}}$$
Answer :
$$\frac{{16{C_1}}}{{{n_1}{n_2}}}$$
68. Eight drops of mercury of equal radii possessing equal charges combine to form a big drop. Then the capacitance of bigger drop compared to each individual small drop is
A
8 times
B
4 times
C
2 times
D
32 times
Answer :
2 times
69. To obtain $$3\,\mu F$$ capacity from three capacitors of $$2\,\mu F$$ each, they will be arranged.
A
all the three in series
B
all the three in parallel
C
two capacitors in series and the third in parallel with the combination of first two
D
two capacitors in parallel and the third in series with the combination of first two
Answer :
two capacitors in series and the third in parallel with the combination of first two
70. A parallel plate condenser has a uniform electric field $$E\left( {\frac{V}{m}} \right)$$ in the space between the plates. If the distance between the plates is $$d\left( m \right)$$ and area of each plate is $$A\left( {{m^2}} \right),$$ the energy (joule) stored in the condenser is
A
$$\frac{1}{2}{\varepsilon _0}{E^2}$$
B
$${\varepsilon _0}EAd$$
C
$$\frac{1}{2}{\varepsilon _0}{E^2}Ad$$
D
$$\frac{{{E^2}Ad}}{{{\varepsilon _0}}}$$
Answer :
$$\frac{1}{2}{\varepsilon _0}{E^2}Ad$$