11. The energy required to charge a parallel plate condenser of plate separation $$d$$ and plate area of cross-section $$A$$ such that the uniform electric field between the plates $$E,$$ is
A
$$\frac{1}{2}\frac{{{\varepsilon _0}{E^2}}}{{Ad}}$$
B
$$\frac{{{\varepsilon _0}{E^2}}}{{Ad}}$$
C
$${\varepsilon _0}{E^2}Ad$$
D
$$\frac{1}{2}\frac{{{\varepsilon _0}{E^2}}}{{Ad}}$$
Answer :
$${\varepsilon _0}{E^2}Ad$$
12. When air in a capacitor is replaced by a medium of dielectric constant $$K,$$ the capacity
A
decreases $$K$$ times
B
increases $$K$$ times
C
increases $${K^2}$$ times
D
remains constant
Answer :
increases $$K$$ times
13.
A parallel plate capacitor of area $$A,$$ plate separation $$d$$ and capacitance $$C$$ is filled with three different dielectric materials having dielectric constants $${k_1},{k_2}$$ and $${k_3}$$ as shown. If a single dielectric material is to be used to have the same capacitance $$C$$ in this capacitor, then its dielectric constant $$k$$ is given by

A
$$\frac{1}{K} = \frac{1}{{{K_1}}} + \frac{1}{{{K_2}}} + \frac{1}{{2{K_3}}}$$
B
$$\frac{1}{K} = \frac{1}{{{K_1} + {K_2}}} + \frac{1}{{2{K_3}}}$$
C
$$K = \frac{{{K_1}{K_2}}}{{{K_1} + {K_2}}} + 2{K_3}$$
D
$$K = {K_1} + {K_2} + 2{K_3}$$
Answer :
$$\frac{1}{K} = \frac{1}{{{K_1} + {K_2}}} + \frac{1}{{2{K_3}}}$$
14. A parallel plate air capacitor has capacity $$C,$$ distance of separation between plates is $$d$$ and potential difference $$V$$ is applied between the plates. Force of attraction between the plates of the parallel plate air capacitor is
A
$$\frac{{{C^2}{V^2}}}{{2d}}$$
B
$$\frac{{C{V^2}}}{{2d}}$$
C
$$\frac{{C{V^2}}}{d}$$
D
$$\frac{{{C^2}{V^2}}}{{2{d^2}}}$$
Answer :
$$\frac{{C{V^2}}}{{2d}}$$
15.
The effective capacitance of combination of equal capacitors between points $$A$$ and $$B$$ shown in figure is

A
$$C$$
B
$$2\,C$$
C
$$3\,C$$
D
$$\frac{C}{2}$$
Answer :
$$2\,C$$
16.
For the circuit shown in Figure, which of the following statements is true?
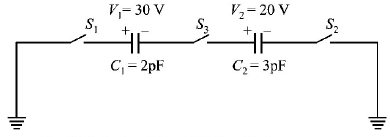
A
With $${S_1}$$ closed $${V_1} = 15\,V,{V_2} = 20\,V$$
B
With $${S_3}$$ closed $${V_1} = {V_2} = 25\,V$$
C
With $${S_1}$$ and $${S_2}$$ closed, $${V_1} = {V_2} = 0$$
D
With $${S_1}$$ and $${S_3}$$ closed, $${V_1} = 30\,V,{V_2} = 20\,V$$
Answer :
With $${S_1}$$ and $${S_3}$$ closed, $${V_1} = 30\,V,{V_2} = 20\,V$$
17. A capacitor of capacity $${C_1}$$ is charged upto potential $$V$$ volt and then connected in parallel to an uncharged capacitor of capacity $${C_2}.$$ The final potential difference across each capacitor will be
A
$$\frac{{{C_2}V}}{{{C_1} + {C_2}}}$$
B
$$\frac{{{C_1}V}}{{{C_1} + {C_2}}}$$
C
$$\left( {1 + \frac{{{C_2}}}{{{C_1}}}} \right)V$$
D
$$\left( {1 - \frac{{{C_2}}}{{{C_1}}}} \right)V$$
Answer :
$$\frac{{{C_1}V}}{{{C_1} + {C_2}}}$$
18.
A parallel plate capacitor is made of two square plates of
side $$'a',$$ separated by a distance $$d\left( {d < < a} \right).$$ The lower triangular portion is filled with a dielectric of dielectric constant $$K,$$ as shown in the figure. Capacitance of this capacitor is:

A
$$\frac{{K{ \in _0}{a^2}}}{{2d\left( {K + 1} \right)}}$$
B
$$\frac{{K{ \in _0}{a^2}}}{{d\left( {K - 1} \right)}}\ell n\,K$$
C
$$\frac{{K{ \in _0}{a^2}}}{d}\ell n\,K$$
D
$$\frac{1}{2}\frac{{K{ \in _0}{a^2}}}{d}$$
Answer :
$$\frac{{K{ \in _0}{a^2}}}{{d\left( {K - 1} \right)}}\ell n\,K$$
19. A parallel plate air capacitor has a capacitance of $$100\,\mu F.$$ The plates are at a distance $$d$$ apart. If a slab of thickness $$t\left( {t < d} \right)$$ and dielectric constant $$5$$ is introduced between the parallel plates, then the capacitance will be
A
$$50\,\mu F$$
B
$$100\,\mu F$$
C
$$200\,\mu F$$
D
$$500\,\mu F$$
Answer :
$$200\,\mu F$$
20.
A parallel plate capacitor $$C$$ with plates of unit area and separation $$d$$ is filled with a liquid of dielectric constant $$K = 2.$$ The level of liquid is $$\frac{d}{3}$$ initially. Suppose the liquid level decreases at a constant speed $$v,$$ the time constant as a function of time $$t$$ is-

A
$$\frac{{6{\varepsilon _0}R}}{{5d + 3vt}}$$
B
$$\frac{{\left( {15d + 9vt} \right){\varepsilon _0}R}}{{2{d^2} - 3dvt - 9{v^2}{t^2}}}$$
C
$$\frac{{6{\varepsilon _0}R}}{{5d - 3vt}}$$
D
$$\frac{{\left( {15d - 9vt} \right){\varepsilon _0}R}}{{2{d^2} - 3dvt - 9{v^2}{t^2}}}$$
Answer :
$$\frac{{6{\varepsilon _0}R}}{{5d + 3vt}}$$




