51.
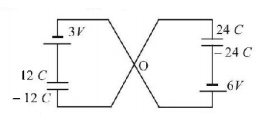
A network of four capacitors of capacity equal to $${C_1} = C,{C_2} = 2C,{C_3} = 3C$$ and $${C_4} = 4C$$ are connected to a battery as shown in the figure. The ratio of the charges on $${C_2}$$ and $${C_4}$$ is

A
$$\frac{{22}}{3}$$
B
$$\frac{3}{{22}}$$
C
$$\frac{7}{4}$$
D
$$\frac{4}{7}$$
Answer :
$$\frac{{22}}{3}$$
52. A parallel plate capacitor of capacitance $$C$$ is connected to a battery and is charged to a potential difference $$V.$$ Another capacitor of capacitance $$2C$$ is similarly charged to a potential difference $$2V.$$ The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the positive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is
A
zero
B
$$\frac{3}{2}C{V^2}$$
C
$$\frac{{25}}{6}C{V^2}$$
D
$$\frac{9}{2}C{V^2}$$
Answer :
$$\frac{3}{2}C{V^2}$$
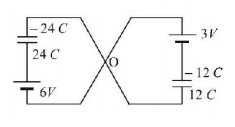
53.
In figure, there is a four way key at the middle. If key is shown from situation $$BD$$ to $$AD,$$ then how much charge will flow through point $$O$$ ?
A
$$24\,\mu C$$
B
$$36\,\mu C$$
C
$$72\,\mu C$$
D
$$12\,\mu C$$
Answer :
$$72\,\mu C$$
54. A small signal voltage $$V\left( t \right) = {V_0}\sin \omega t$$ is applied across an ideal capacitor $$C$$
A
over a full cycle the capacitor $$C$$ does not consume any energy from the voltage source
B
current $$l\left( t \right)$$ is in phase with voltage $$V\left( t \right)$$
C
current $$l\left( t \right)$$ leads voltage $$V\left( t \right)$$ by $${180^ \circ }$$
D
current $$l\left( t \right),$$ lags voltage $$V\left( t \right)$$ by $${90^ \circ }$$
Answer :
over a full cycle the capacitor $$C$$ does not consume any energy from the voltage source
55. The capacitance of a metallic sphere is $$1\,\mu F,$$ then it's radius is nearly
A
$$1.11\,m$$
B
$$10\,m$$
C
$$9\,km$$
D
$$1.11\,cm$$
Answer :
$$9\,km$$
56. A parallel plate capacitor of capacitance $$90pF$$ is connected to a battery of emf $$20V.$$ If a dielectric material of dielectric constant $$k = \frac{5}{3}$$ is inserted between the plates, the magnitude of the induced charge will be:
A
$$1.2\,nC$$
B
$$0.3\,n C$$
C
$$2.4\,n C$$
D
$$0.9\,n C$$
Answer :
$$1.2\,nC$$
57. A parallel plate capacitor with air between the plates has capacitance of 9 $$pF.$$ The separation between its plates is $$'d'.$$ The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant $${k_1} = 3$$ and thickness $${\frac{d}{3}}$$ while the other one has dielectric constant $${k_2} = 6$$ and thickness $$\frac{{2d}}{3}.$$ Capacitance of the capacitor is now
A
1.8 $$pF$$
B
45 $$pF$$
C
40.5 $$pF$$
D
20.25 $$pF$$
Answer :
40.5 $$pF$$
58.
The four capacitors, each of $$25\mu F$$ are connected as shown in figure. The $$DC$$ voltmeter reads $$200\,V.$$ The charge on each plate of capacitor is
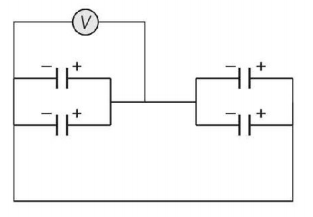
A
$$ \pm 2 \times {10^{ - 3}}C$$
B
$$ \pm 5 \times {10^{ - 3}}C$$
C
$$ \pm 2 \times {10^{ - 2}}C$$
D
$$ \pm 5 \times {10^{ - 2}}C$$
Answer :
$$ \pm 5 \times {10^{ - 3}}C$$
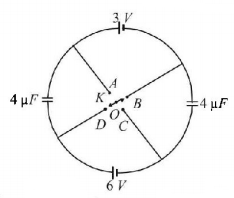
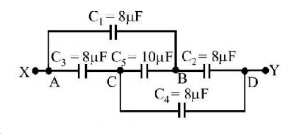
59.
What is the effective capacitance between points $$X$$ and $$Y$$?
A
$$8\,\mu F$$
B
$$9\,\mu F$$
C
$$10\,\mu F$$
D
$$12\,\mu F$$
Answer :
$$8\,\mu F$$
60. A $$4\mu F$$ capacitor is charged to $$400\,V$$ and then its plates are joined through a resistance of $$1\,k\Omega .$$ The heat produced in the resistance is
A
$$0.16\,J$$
B
$$1.28\,J$$
C
$$0.64\,J$$
D
$$0.32\,J$$
Answer :
$$0.32\,J$$