161. A man places a chain of mass $$m$$ and length $$L$$ on a table slowly. Initially the lower end of the chain just touches the table. The man drops the chain when half of the chain is in vertical position. Then work done by the man in this process is
A
$$ - mg\frac{L}{2}$$
B
$$ - \frac{{mgL}}{4}$$
C
$$ - \frac{{3mgL}}{8}$$
D
$$ - \frac{{mgL}}{8}$$
Answer :
$$ - \frac{{3mgL}}{8}$$
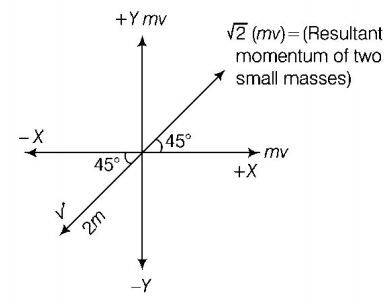
162. A body of mass $$\left( {4m} \right)$$ is lying in $$xy$$ -plane at rest. It suddenly explodes into three pieces. Two pieces each of mass $$\left( {m} \right)$$ move perpendicular to each other with equal speeds $$\left( {v} \right).$$ The total kinetic energy generated due to explosion is
A
$$m{v^2}$$
B
$$\frac{3}{2}m{v^2}$$
C
$$2m{v^2}$$
D
$$4m{v^2}$$
Answer :
$$\frac{3}{2}m{v^2}$$
163. Water falls from a height of $$60\,m$$ at the rate of $$15\,kg/s$$ to operate a turbine. The losses due to frictional forces are $$10\% $$ of energy. How much power is generated by the turbine ? (Take $$g = 10\,m/{s^2}$$ )
A
$$8.1\,kW$$
B
$$10.2\,kW$$
C
$$12.3\,kW$$
D
$$7.0\,kW$$
Answer :
$$8.1\,kW$$
164. Work done by static friction on an object
A
maybe positive
B
must be negative
C
must be zero
D
None of these
Answer :
maybe positive
165.
A ball of mass $$m$$ hits the floor making an angle $$\theta $$ as shown in the figure. If $$e$$ is the coefficient of restitution, then which relation is true, for the velocity component before and after collision?
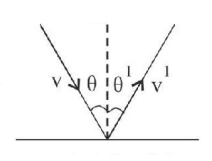
A
$${V^1}\sin \theta ' = V\sin \theta $$
B
$${V^1}\sin \theta ' = - \sin \theta $$
C
$${V^1}\cos \theta ' = V\cos \theta $$
D
$${V^1}\cos \theta ' = - V\cos \theta $$
Answer :
$${V^1}\sin \theta ' = V\sin \theta $$
166.
How much water a pump of $$2\,kW$$ can raise in one minute to a height of $$10\,m$$ ?
(Take $$g = 10\,m/{s^2}$$ )
A
$$1000\,L$$
B
$$1200\,L$$
C
$$100\,L$$
D
$$2000\,L$$
Answer :
$$1200\,L$$
167. $$300\,J$$ of work is done in sliding a $$2\,kg$$ block up an inclined plane of height $$10\,m.$$ Taking $$g = 10\,m/{s^2},$$ work done against friction is
A
$$200\,J$$
B
$$100\,J$$
C
zero
D
$$1000\,J$$
Answer :
$$100\,J$$
168.
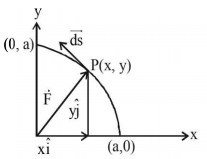
The work done on a particle of mass $$m$$ by a force,
$$K\left[ {\frac{x}{{{{\left( {{x^2} + {y^2}} \right)}^{\frac{3}{2}}}}}\hat i + \frac{y}{{{{\left( {{x^2} + {y^2}} \right)}^{\frac{3}{2}}}}}\hat j} \right]$$
($$K$$ being a constant of appropriate dimensions), when the particle is taken from the point ($$a, 0$$ ) to the point ($$0, a$$ ) along a circular path of radius $$a$$ about the origin in the $$x-y$$ plane is-
A
$$\frac{{2K\pi }}{a}$$
B
$$\frac{{K\pi }}{a}$$
C
$$\frac{{K\pi }}{2a}$$
D
$$0$$
Answer :
$$0$$
169. A body of mass $$m = {10^{ - 2}}\,kg$$ is moving in a medium and experiences a frictional force $$F = - k{v^2}.$$ Its initial speed is $${v_0} = 10\,m{s^{ - 1}}.$$ If, after $$10 \,s,$$ its energy is $$\frac{1}{8}mv_0^2,$$ the value of $$k$$ will be-
A
$${10^{ - 4}}\,kg\,{m^{ - 1}}$$
B
$${10^{ - 1}}\,kg\,{m^{ - 1}}{s^{ - 1}}$$
C
$${10^{ - 3}}\,kg\,{m^{ - 1}}$$
D
$${10^{ - 3}}\,kg\,{s^{ - 1}}$$
Answer :
$${10^{ - 4}}\,kg\,{m^{ - 1}}$$
170. A particle is moving in a circular path of radius a under the action of an attractive potential $$U = - \frac{k}{{2{r^2}}}.$$ Its total energy is:
A
$$ - \frac{k}{{4{a^2}}}$$
B
$$\frac{k}{{2{a^2}}}$$
C
$$Zero$$
D
$$ - \frac{3}{2}\frac{k}{{{a^2}}}$$
Answer :
$$Zero$$