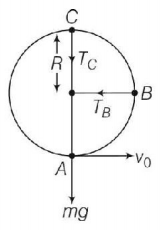
121. What is the minimum velocity with which a body of mass $$m$$ must enter a vertical loop of radius $$R$$ so that it can complete the loop?
A
$$\sqrt {2gR} $$
B
$$\sqrt {3gR} $$
C
$$\sqrt {5gR} $$
D
$$\sqrt {gR} $$
Answer :
$$\sqrt {5gR} $$
122. The potential energy of a particle in a force field is $$U = \frac{A}{{{r^2}}} - \frac{B}{r},$$ where $$A$$ and $$B$$ are positive constants and $$r$$ is the distance of particle from the centre of the field. For stable equilibrium, the distance of the particle is
A
$$\frac{B}{{2A}}$$
B
$$\frac{{2A}}{B}$$
C
$$\frac{A}{B}$$
D
$$\frac{B}{A}$$
Answer :
$$\frac{{2A}}{B}$$
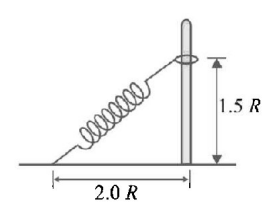
123.
A ring of mass $$m$$ can slide over a smooth vertical rod as shown in figure. The ring is connected to a spring of force constant $$k = 4\,mg/R,$$ where $$2R$$ is the natural length of the spring. The other end of spring is fixed to the ground at a horizontal distance $$2R$$ from the base of the rod. If the mass is released at a height $$1.5\,R,$$ then the velocity of the ring as it reaches the ground is
A
$$\sqrt {gR} $$
B
$$2\sqrt {gR} $$
C
$$\sqrt {2gR} $$
D
$$\sqrt {3gR} $$
Answer :
$$2\sqrt {gR} $$
124. A particle describe a horizontal circle of radius $$0.5\,m$$ with uniform speed. The centripetal force acting is $$10\,N.$$ The work done in describing a semicircle is
A
zero
B
$$5\,J$$
C
$$5\,\pi J$$
D
$$10\,\pi J$$
Answer :
zero
125. $$300\,J$$ of work is done in sliding a $$2\,kg$$ block up an inclined plane of height $$10\,m.$$ Taking $$g = 10\,m/{s^2},$$ work done against friction is
A
$$100\,J$$
B
zero
C
$$1000\,J$$
D
$$200\,J$$
Answer :
$$100\,J$$
126. A uniform cable of mass $$'M ’$$ and length $$'L ’$$ is placed on a horizontal surface such that its $${\left( {\frac{1}{n}} \right)^{th}}$$ part is hanging below the edge of the surface. To lift the hanging part of the cable upto the surface, the work done should be:
A
$$\frac{{MgL}}{{2{n^2}}}$$
B
$$\frac{{MgL}}{{{n^2}}}$$
C
$$\frac{{2MgL}}{{{n^2}}}$$
D
$$nMgL$$
Answer :
$$\frac{{MgL}}{{{n^2}}}$$
127. Two bodies with kinetic energies in the ratio $$4:1$$ are moving with equal linear momentum. The ratio of their masses is
A
$$1:2$$
B
$$1:1$$
C
$$4:1$$
D
$$1:4$$
Answer :
$$1:4$$
128.
A man starts walking from a point on the surface of earth (assumed smooth) and reaches diagonally opposite point.
What is the work done by him?
A
Zero
B
Positive
C
Negative
D
Nothing can be said
Answer :
Zero
129. A body starts from rest and acquires a velocity $$V$$ in time $$T.$$ The work done on the body in time $$t$$ will be proportional to
A
$$\frac{V}{T}t$$
B
$$\frac{{{V^2}}}{T}{t^2}$$
C
$$\frac{{{V^2}}}{{{T^2}}}t$$
D
$$\frac{{{V^2}}}{{{T^2}}}{t^2}$$
Answer :
$$\frac{{{V^2}}}{{{T^2}}}{t^2}$$
130. A uniform force of $$\left( {3\hat i + \hat j} \right)N$$ acts on a particle of mass $$2\,kg.$$ Hence, the particle is displaced from position $$\left( {2\hat i + \hat k} \right)m$$ to position $$\left( {4\hat i + 3\hat j - \hat k} \right)m.$$ The work done by the force on the particle is
A
$$9\,J$$
B
$$6\,J$$
C
$$13\,J$$
D
$$15\,J$$
Answer :
$$9\,J$$