11. If $$n$$ bullets each of mass $$m$$ are fired with a velocity $$v$$ per second from a machine gun, the force required to hold the gun in position is
A
$$\left( {n + 1} \right)mv$$
B
$$\frac{{mv}}{{{n^2}}}$$
C
$$\frac{{mv}}{n}$$
D
$$mnv$$
Answer :
$$mnv$$
12.
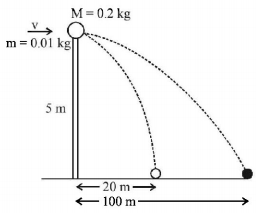
A ball of mass $$0.2kg$$ rests on a vertical post of height $$5m.$$ A bullet of mass $$0.01kg,$$ traveling with a velocity $$V m/s$$ in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of $$20m$$ and the bullet at a distance of $$100m$$ from the foot of the post. The velocity $$V$$ of the bullet is
A
$$250 m/s$$
B
$$250\sqrt 2 \,m/s$$
C
$$400 m/s$$
D
$$500 m/s$$
Answer :
$$500 m/s$$
13. Sand is being dropped on a conveyor belt at the rate of $$M\,kg/s.$$ The force (in $$N$$) necessary to keep the belt moving with a constant velocity of $$v\,m/s$$ will be:
A
$$Mv$$
B
$$2\,Mv$$
C
$$\frac{{Mv}}{2}$$
D
$$\frac{{Mv}}{3}$$
Answer :
$$Mv$$
14. A $$5000\,kg$$ rocket is set for vertical firing. The exhaust speed is $$800\,m{s^{ - 1}}.$$ To give an initial upward acceleration of $$20\,m{s^{ - 2}},$$ the amount of gas ejected per second to supply the needed thrust will be $$\left( {g = 10\,m{s^{ - 2}}} \right)$$
A
$$127.5\,kg\,{s^{ - 1}}$$
B
$$187.5\,kg\,{s^{ - 1}}$$
C
$$185.5\,kg\,{s^{ - 1}}$$
D
$$137.5\,kg\,{s^{ - 1}}$$
Answer :
$$187.5\,kg\,{s^{ - 1}}$$
15. The force on a rocket moving with a velocity $$300\,m/s$$ is $$210\,N.$$ The rate of consumption of fuel of rocket is
A
$$0.7\,kg/s$$
B
$$1.4\,kg/s$$
C
$$0.07\,kg/s$$
D
$$10.7\,kg/s$$
Answer :
$$0.7\,kg/s$$
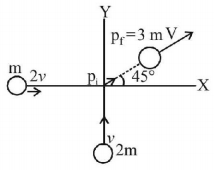
16. A particle of mass $$m$$ moving in the $$x$$ direction with speed $$2v$$ is hit by another particle of mass $$2m$$ moving in the $$y$$ direction with speed $$v.$$ If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:
A
56%
B
62%
C
44%
D
50%
Answer :
56%
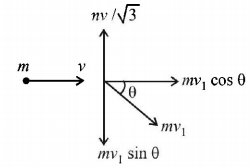
17.
A mass $$'m'$$ moves with a velocity $$'v'$$ and collides inelastically with another identical mass . After collision the $${1^{st}}$$ mass moves with velocity $$\frac{v}{{\sqrt 3 }}$$ in a direction perpendicular to the initial direction of motion. Find the speed of the $${2^{nd}}$$ mass after collision.
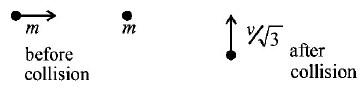
A
$$\sqrt 3 v$$
B
$$v$$
C
$$\frac{v}{{\sqrt 3 }}$$
D
$$\frac{2}{{\sqrt 3 }}v$$
Answer :
$$\frac{2}{{\sqrt 3 }}v$$
18. A bullet of mass $$10\,g$$ moving horizontal with a velocity of $$400\,m/s$$ strikes a wood block of mass $$2\,kg$$ which is suspended by light inextensible string of length $$5 m.$$ As result, the centre of gravity of the block found to rise a vertical distance of $$10\,cm.$$ The speed of the bullet after it emerges of horizontally from the block will be
A
$$100\,m/s$$
B
$$80\,m/s$$
C
$$120\,m/s$$
D
$$160\,m/s$$
Answer :
$$120\,m/s$$
19. A satellite in a force free space sweeps stationary interplanetary dust at a rate $$\left( {\frac{{dM}}{{dt}}} \right) = \alpha v.$$ The acceleration of satellite is
A
$$\frac{{ - 2\alpha {v^2}}}{M}$$
B
$$\frac{{ - \alpha {v^2}}}{M}$$
C
$$\frac{{ - \alpha {v^2}}}{{2M}}$$
D
$$ - \alpha {v^2}$$
Answer :
$$\frac{{ - \alpha {v^2}}}{M}$$
20. A stone is dropped from a height $$h.$$ It hits the ground with a certain momentum $$P.$$ If the same stone is dropped from a height $$100\% $$ more than the previous height, the momentum when it hits the ground will change by :
A
$$68\% $$
B
$$41\% $$
C
$$200\% $$
D
$$100\% $$
Answer :
$$41\% $$