Question
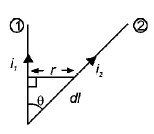
Wires 1 and 2 carrying currents $${i_1}$$ and $${i_2}$$ respectively are inclined at an angle $$\theta $$ to each other. What is the force on a small element $$dl$$ of wire 2 at a distance of $$r$$ from wire 1 (as shown in figure) due to the magnetic field of wire 1?
Wires 1 and 2 carrying currents $${i_1}$$ and $${i_2}$$ respectively are inclined at an angle $$\theta $$ to each other. What is the force on a small element $$dl$$ of wire 2 at a distance of $$r$$ from wire 1 (as shown in figure) due to the magnetic field of wire 1?
A.
$$\frac{{{\mu _0}}}{{2\pi r}}{i_1}{i_2}dl\tan \theta $$
B.
$$\frac{{{\mu _0}}}{{2\pi r}}{i_1}{i_2}dl\sin \theta $$
C.
$$\frac{{{\mu _0}}}{{2\pi r}}{i_1}{i_2}dl\cos \theta $$
D.
$$\frac{{{\mu _0}}}{{4\pi r}}{i_1}{i_2}dl\sin \theta $$
Answer :
$$\frac{{{\mu _0}}}{{2\pi r}}{i_1}{i_2}dl\cos \theta $$
Solution :
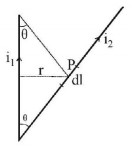
Magnetic field due to current in wire 1 at point $$P$$ distant $$r$$ from the wire is
$$\eqalign{ & B = \frac{{{\mu _0}}}{{4\pi }}\frac{{{i_1}}}{r}\left[ {\cos \theta + \cos \theta } \right] \cr & B = \frac{{{\mu _0}}}{{2\pi }}\frac{{{i_1}\cos \theta }}{r}\,\left( {{\text{directed perpendicular to the plane of paper, inwards}}} \right) \cr} $$
The force exerted due to this magnetic field on current element $${i_2}dl$$ is $$dF = {i_2}dl\sin {90^ \circ }$$
$$\therefore dF = {i_2}dl\left[ {\frac{{{\mu _0}}}{{2\pi }}\frac{{{i_1}\cos \theta }}{r}} \right] = \frac{{{\mu _0}}}{{2\pi }}{i_1}{i_2}dl\cos \theta $$

Magnetic field due to current in wire 1 at point $$P$$ distant $$r$$ from the wire is
$$\eqalign{ & B = \frac{{{\mu _0}}}{{4\pi }}\frac{{{i_1}}}{r}\left[ {\cos \theta + \cos \theta } \right] \cr & B = \frac{{{\mu _0}}}{{2\pi }}\frac{{{i_1}\cos \theta }}{r}\,\left( {{\text{directed perpendicular to the plane of paper, inwards}}} \right) \cr} $$
The force exerted due to this magnetic field on current element $${i_2}dl$$ is $$dF = {i_2}dl\sin {90^ \circ }$$
$$\therefore dF = {i_2}dl\left[ {\frac{{{\mu _0}}}{{2\pi }}\frac{{{i_1}\cos \theta }}{r}} \right] = \frac{{{\mu _0}}}{{2\pi }}{i_1}{i_2}dl\cos \theta $$