Question
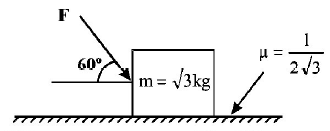
What is the maximum value of the force $$F$$ such that the block shown in the arrangement, does not move?
What is the maximum value of the force $$F$$ such that the block shown in the arrangement, does not move?
A.
$$20\,N$$
B.
$$10\,N$$
C.
$$12\,N$$
D.
$$15\,N$$
Answer :
$$20\,N$$
Solution :
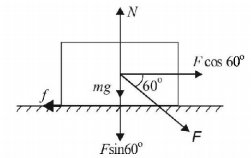
The forces acting on the block are shown. Since the block is not moving forward for the maximum force $$F$$ applied, therefore
$$F\cos {60^ \circ } = f = \mu N\,......\left( {\text{i}} \right)$$ (Horizontal Direction)
Note : For maximum force $$F,$$ the frictional force is the limiting friction $$ = \left. {\mu N} \right]$$
and $$F\sin {60^ \circ } + mg = N\,......\left( {{\text{ii}}} \right)$$
From (i) and (ii)
$$\eqalign{ & F\cos {60^ \circ } = \mu \left[ {F\sin {{60}^ \circ } + mg} \right] \cr & \Rightarrow F = \frac{{\mu mg}}{{\cos {{60}^ \circ } - \mu \sin {{60}^ \circ }}} \cr & = \frac{{\frac{1}{{2\sqrt 3 }} \times \sqrt 3 \times 10}}{{\frac{1}{2} - \frac{1}{{2\sqrt 3 }} \times \frac{{\sqrt 3 }}{2}}} = \frac{5}{{\frac{1}{4}}} = 20N \cr} $$
The forces acting on the block are shown. Since the block is not moving forward for the maximum force $$F$$ applied, therefore
$$F\cos {60^ \circ } = f = \mu N\,......\left( {\text{i}} \right)$$ (Horizontal Direction)
Note : For maximum force $$F,$$ the frictional force is the limiting friction $$ = \left. {\mu N} \right]$$
and $$F\sin {60^ \circ } + mg = N\,......\left( {{\text{ii}}} \right)$$
From (i) and (ii)

$$\eqalign{ & F\cos {60^ \circ } = \mu \left[ {F\sin {{60}^ \circ } + mg} \right] \cr & \Rightarrow F = \frac{{\mu mg}}{{\cos {{60}^ \circ } - \mu \sin {{60}^ \circ }}} \cr & = \frac{{\frac{1}{{2\sqrt 3 }} \times \sqrt 3 \times 10}}{{\frac{1}{2} - \frac{1}{{2\sqrt 3 }} \times \frac{{\sqrt 3 }}{2}}} = \frac{5}{{\frac{1}{4}}} = 20N \cr} $$
