Question
Two small particles of equal masses start moving in opposite directions from a point $$A$$ in a horizontal circular orbit. Their tangential velocities are $$v$$ and $$2v,$$ respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at $$A,$$ these two particles will again reach the point $$A$$ ?
Two small particles of equal masses start moving in opposite directions from a point $$A$$ in a horizontal circular orbit. Their tangential velocities are $$v$$ and $$2v,$$ respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at $$A,$$ these two particles will again reach the point $$A$$ ?
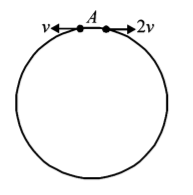
A.
4
B.
3
C.
2
D.
1
Answer :
2
Solution :
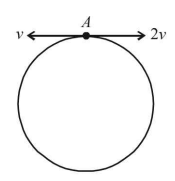
Let the radius of the circle be $$r.$$ Then the two distance travelled by the two particles before first collision is $$2\pi r.$$ Therefore $$2v \times t + v \times t = 2\pi r$$ where $$t$$ is the time taken for first collision to occur.
$$\therefore t = \frac{{2\pi r}}{{3v}}$$
$$\therefore $$ Distance travelled by particle with velocity $$v$$ is equal to $$v \times \frac{{2\pi r}}{{3v}} = \frac{{2\pi r}}{3}.$$
Therefore the collision occurs at $$B.$$
.PNG)
As the collision is elastic and the particles have equal masses, the velocities will interchange as shown in the figure. According to the same reasoning as above, the 2nd collision will take place at $$C$$ and the velocities will again interchange.
With the same reasoning the 3rd collision will occur at the point $$A.$$ Thus there will be two elastic collisions before the particles again reach at $$A.$$

Let the radius of the circle be $$r.$$ Then the two distance travelled by the two particles before first collision is $$2\pi r.$$ Therefore $$2v \times t + v \times t = 2\pi r$$ where $$t$$ is the time taken for first collision to occur.
$$\therefore t = \frac{{2\pi r}}{{3v}}$$
$$\therefore $$ Distance travelled by particle with velocity $$v$$ is equal to $$v \times \frac{{2\pi r}}{{3v}} = \frac{{2\pi r}}{3}.$$
Therefore the collision occurs at $$B.$$
.PNG)
As the collision is elastic and the particles have equal masses, the velocities will interchange as shown in the figure. According to the same reasoning as above, the 2nd collision will take place at $$C$$ and the velocities will again interchange.
With the same reasoning the 3rd collision will occur at the point $$A.$$ Thus there will be two elastic collisions before the particles again reach at $$A.$$