Question
Two simple harmonic motions given by,
Two simple harmonic motions given by,
$$x = a\sin \left( {\omega t + \delta } \right)$$ and $$y = a\sin $$
$$\left( {\omega t + \delta + \frac{\pi }{2}} \right)$$ act on a particle simultaneously, then the motion of particle will be
A.
circular anti-clockwise
B.
circular clockwise
C.
elliptical anti-clockwise
D.
elliptical clockwise
Answer :
circular clockwise
Solution :
Two simple harmonic motions can be written as
$$\eqalign{ & x = a\sin \left( {\omega t + \delta } \right)\,......\left( {\text{i}} \right) \cr & {\text{and}}\,\,y = a\sin \left( {\omega t + \delta + \frac{\pi }{2}} \right) \cr & {\text{or}}\,\,y = a\cos \left( {\omega t + \delta } \right)\,......\left( {{\text{ii}}} \right) \cr} $$
Squaring and adding Eqs. (i) and (ii), we obtain
$$\eqalign{ & {x^2} + {y^2} = {a^2}\left[ {{{\sin }^2}\left( {\omega t + \delta } \right) + {{\cos }^2}\left( {\omega t + \delta } \right)} \right] \cr & {\text{or}}\,\,{x^2} + {y^2} = {a^2}\,\,\left( {\because {{\sin }^2}\theta + {{\cos }^2}\theta = 1} \right) \cr} $$
This is the equation of a circle.
$$\eqalign{ & {\text{At}}\,\,\left( {\omega t + \delta } \right) = 0;x = 0,y = a \cr & {\text{At}}\,\,\left( {\omega t + \delta } \right) = \frac{\pi }{2};x = a,y = 0 \cr & {\text{At}}\,\,\left( {\omega t + \delta } \right) = \pi ;x = 0,y = - a \cr & {\text{At}}\,\,\left( {\omega t + \delta } \right) = \frac{{3\pi }}{2};x = - a,y = 0 \cr & {\text{At}}\,\,\left( {\omega t + \delta } \right) = 2\pi ;x = 0,y = a \cr} $$
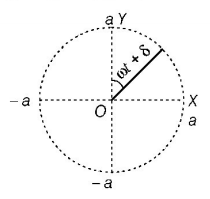
Thus, it is obvious that motion of particle is traversed in clockwise direction.
Two simple harmonic motions can be written as
$$\eqalign{ & x = a\sin \left( {\omega t + \delta } \right)\,......\left( {\text{i}} \right) \cr & {\text{and}}\,\,y = a\sin \left( {\omega t + \delta + \frac{\pi }{2}} \right) \cr & {\text{or}}\,\,y = a\cos \left( {\omega t + \delta } \right)\,......\left( {{\text{ii}}} \right) \cr} $$
Squaring and adding Eqs. (i) and (ii), we obtain
$$\eqalign{ & {x^2} + {y^2} = {a^2}\left[ {{{\sin }^2}\left( {\omega t + \delta } \right) + {{\cos }^2}\left( {\omega t + \delta } \right)} \right] \cr & {\text{or}}\,\,{x^2} + {y^2} = {a^2}\,\,\left( {\because {{\sin }^2}\theta + {{\cos }^2}\theta = 1} \right) \cr} $$
This is the equation of a circle.
$$\eqalign{ & {\text{At}}\,\,\left( {\omega t + \delta } \right) = 0;x = 0,y = a \cr & {\text{At}}\,\,\left( {\omega t + \delta } \right) = \frac{\pi }{2};x = a,y = 0 \cr & {\text{At}}\,\,\left( {\omega t + \delta } \right) = \pi ;x = 0,y = - a \cr & {\text{At}}\,\,\left( {\omega t + \delta } \right) = \frac{{3\pi }}{2};x = - a,y = 0 \cr & {\text{At}}\,\,\left( {\omega t + \delta } \right) = 2\pi ;x = 0,y = a \cr} $$

Thus, it is obvious that motion of particle is traversed in clockwise direction.