Releted MCQ Question on
Heat and Thermodynamics >> Thermal Expansion
Releted Question 1
A metal ball immersed in alcohol weighs $${W_1}$$ at $${0^ \circ }C$$ and $${W_2}$$ at $${50^ \circ }C.$$ The co-efficient of expansion of cubical the metal is less than that of the alcohal. Assuming that the density of the metal is large compared to that of alcohol, it can be shown that
A.
$${W_1} > {W_2}$$
B.
$${W_1} = {W_2}$$
C.
$${W_1} < {W_2}$$
D.
None of these
Releted Question 2
Two rods, one of aluminum and the other made of steel, having initial length $${\ell _1}$$ and $${\ell _2}$$ are connected together to form a single rod of length $${{\ell _1} + {\ell _2}}.$$ The co-efficients of linear expansion for aluminum and steel are $${\alpha _a}$$ and $${\alpha _s}$$ and respectively. If the length of each rod increases by the same amount when their temperature are raised by $${t^ \circ }C,$$ then find the ratio $$\frac{{{\ell _1}}}{{\left( {{\ell _1} + {\ell _2}} \right)}}$$
A.
$$\frac{{{\alpha _s}}}{{{\alpha _a}}}$$
B.
$$\frac{{{\alpha _a}}}{{{\alpha _s}}}$$
C.
$$\frac{{{\alpha _s}}}{{\left( {{\alpha _a} + {\alpha _s}} \right)}}$$
D.
$$\frac{{{\alpha _a}}}{{\left( {{\alpha _a} + {\alpha _s}} \right)}}$$
Releted Question 3
Statement - 1 : The temperature dependence of resistance is usually given as $$R = {R_0}\left( {1 + \alpha \,\Delta t} \right).$$ The resistance of a wire changes from $$100\,\Omega $$ to $$150\,\Omega $$ when its emperature is increased from $${27^ \circ }C$$ to $${227^ \circ }C.$$ This implies that $$\alpha = \frac{{2.5 \times {{10}^{ - 3}}}}{{^ \circ C}}.$$
Statement - 1 : The temperature dependence of resistance is usually given as $$R = {R_0}\left( {1 + \alpha \,\Delta t} \right).$$ The resistance of a wire changes from $$100\,\Omega $$ to $$150\,\Omega $$ when its emperature is increased from $${27^ \circ }C$$ to $${227^ \circ }C.$$ This implies that $$\alpha = \frac{{2.5 \times {{10}^{ - 3}}}}{{^ \circ C}}.$$
Statement - 2 : $$R = {R_0}\left( {1 + \alpha \,\Delta t} \right)$$ is valid only when the change in the temperature $${\Delta T}$$ is small and $$\Delta R = \left( {R - {R_0}} \right) \ll {R_0}.$$
A.
Statement - 1 is true, Statement - 2 is true; Statement - 2 is the correct explanation of Statement - 1.
B.
Statement - 1 is true, Statement - 2 is true; Statement - 2 is not the correct explanation of Statement - 1.
C.
Statement - 1 is false, Statement - 2 is true.
D.
Statement - 1 is true, Statement - 2 is false.
Releted Question 4
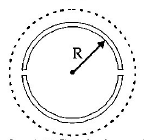
A wooden wheel of radius $$R$$ is made of two semicircular part (see figure). The two parts are held together by a ring made of a metal strip of cross sectional area $$S$$ and length $$L. L$$ is slightly less than $$2\,\pi R.$$ To fit the ring on the wheel, it is heated so that its temperature rises by $$\Delta T$$ and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the co-efficient of linear expansion of the metal is $$\alpha ,$$ and its Young's modulus is $$Y,$$ the force that one part of the wheel applies on the other part is :
A wooden wheel of radius $$R$$ is made of two semicircular part (see figure). The two parts are held together by a ring made of a metal strip of cross sectional area $$S$$ and length $$L. L$$ is slightly less than $$2\,\pi R.$$ To fit the ring on the wheel, it is heated so that its temperature rises by $$\Delta T$$ and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the co-efficient of linear expansion of the metal is $$\alpha ,$$ and its Young's modulus is $$Y,$$ the force that one part of the wheel applies on the other part is :
A.
$$2\,\pi SY\alpha \,\Delta T$$
B.
$$SY\alpha \,\Delta T$$
C.
$$\pi SY\alpha \,\Delta T$$
D.
$$2\,SY\alpha \,\Delta T$$