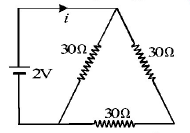
Question
Two rods $$A$$ and $$B$$ of different materials are welded together as shown in figure. Their thermal conductivities are $${K_1}$$ and $${K_2}.$$ The thermal conductivity of the composite rod will be
Two rods $$A$$ and $$B$$ of different materials are welded together as shown in figure. Their thermal conductivities are $${K_1}$$ and $${K_2}.$$ The thermal conductivity of the composite rod will be

A.
$$\frac{{{K_1} + {K_2}}}{2}$$
B.
$$\frac{{3\left( {{K_1} + {K_2}} \right)}}{2}$$
C.
$${K_1} + {K_2}$$
D.
$$2\left( {{K_1} + {K_2}} \right)$$
Answer :
$$\frac{{{K_1} + {K_2}}}{2}$$
Solution :
In parallel arrangement of $$n$$ rods Equivalent thermal conductivity is given by
$${K_{{\text{eq}}}} = \frac{{{K_1}{A_1} + {K_2}{A_2} + \ldots + {K_n}{A_n}}}{{{A_1} + {A_2} + \ldots + {A_n}}}$$
If rods are of same area, then
$${K_{{\text{eq}}}} = \frac{{{K_1} + {K_2} + \ldots + {K_n}}}{n}$$
Now, in the question, it is not given that rods are of same area. But we can judge that from given diagram.
∴ Equivalent thermal conductivity of the system of two rods
$$ \Rightarrow {K_{{\text{eq}}}} = \frac{{{K_1} + {K_2}}}{2}$$
In parallel arrangement of $$n$$ rods Equivalent thermal conductivity is given by
$${K_{{\text{eq}}}} = \frac{{{K_1}{A_1} + {K_2}{A_2} + \ldots + {K_n}{A_n}}}{{{A_1} + {A_2} + \ldots + {A_n}}}$$
If rods are of same area, then
$${K_{{\text{eq}}}} = \frac{{{K_1} + {K_2} + \ldots + {K_n}}}{n}$$
Now, in the question, it is not given that rods are of same area. But we can judge that from given diagram.
∴ Equivalent thermal conductivity of the system of two rods
$$ \Rightarrow {K_{{\text{eq}}}} = \frac{{{K_1} + {K_2}}}{2}$$