Question
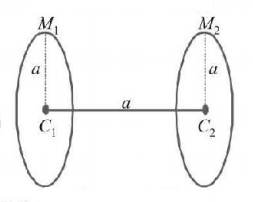
Two rings each of radius $$'a'$$ are coaxial and the distance between their centres is $$a.$$ The masses of the rings are $${M_1}$$ and $${M_2}.$$ The work done in transporting a particle of a small mass $$m$$ from centre $${C_1}$$ to $${C_2}$$ is :
Two rings each of radius $$'a'$$ are coaxial and the distance between their centres is $$a.$$ The masses of the rings are $${M_1}$$ and $${M_2}.$$ The work done in transporting a particle of a small mass $$m$$ from centre $${C_1}$$ to $${C_2}$$ is :
A.
$$\frac{{Gm\left( {{M_2} - {M_1}} \right)}}{a}$$
B.
$$\frac{{Gm\left( {{M_2} - {M_1}} \right)}}{{a\sqrt 2 }}\left( {\sqrt 2 + 1} \right)$$
C.
$$\frac{{Gm\left( {{M_2} - {M_1}} \right)}}{{a\sqrt 2 }}\left( {\sqrt 2 - 1} \right)$$
D.
$$\frac{{Gm\left( {{M_2} - {M_1}} \right)}}{{\sqrt 2 }}a$$
Answer :
$$\frac{{Gm\left( {{M_2} - {M_1}} \right)}}{{a\sqrt 2 }}\left( {\sqrt 2 - 1} \right)$$
Solution :
$$\eqalign{ & W = m\left( {{V_2} - {V_1}} \right) \cr & {\text{when,}}\,{V_1} = - \left[ {\frac{{G{M_1}}}{a} + \frac{{G{M_2}}}{{\sqrt 2 a}}} \right], \cr & {V_2} = - \left[ {\frac{{G{M_2}}}{a} + \frac{{G{M_1}}}{{\sqrt 2 a}}} \right] \cr & \therefore W = \frac{{Gm\left( {{M_2} - {M_1}} \right)}}{{a\sqrt 2 }}\left( {\sqrt 2 - 1} \right). \cr} $$
$$\eqalign{ & W = m\left( {{V_2} - {V_1}} \right) \cr & {\text{when,}}\,{V_1} = - \left[ {\frac{{G{M_1}}}{a} + \frac{{G{M_2}}}{{\sqrt 2 a}}} \right], \cr & {V_2} = - \left[ {\frac{{G{M_2}}}{a} + \frac{{G{M_1}}}{{\sqrt 2 a}}} \right] \cr & \therefore W = \frac{{Gm\left( {{M_2} - {M_1}} \right)}}{{a\sqrt 2 }}\left( {\sqrt 2 - 1} \right). \cr} $$