Question
Two point masses of $$0.3 \,kg$$ and $$0.7 \,kg$$ are fixed at the ends of a rod of length $$1.4 \,m$$ and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of-
A.
$$0.42 \,m$$ from mass of $$0.3 \,kg$$
B.
$$0.70 \,m$$ from mass of $$0.7 \,kg$$
C.
$$0.98 \,m$$ from mass of $$0.3 \,kg$$
D.
$$0.98 \,m$$ from mass of $$0.7 \,kg$$
Answer :
$$0.98 \,m$$ from mass of $$0.3 \,kg$$
Solution :
The moment of inertia of the system about axis of rotation $$O$$ is
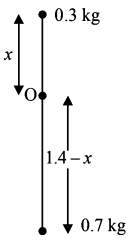
$$\eqalign{ & I = {I_1} + {I_2} = 0.3{x^2} + 0.7{\left( {1.4 - x} \right)^2} \cr & = 0.3{x^2} + 0.7\left( {1.96 + {x^2} - 2.8x} \right) \cr & = {x^2} + 1.372 - 1.96x \cr} $$
The work done in rotating the rod is converted into its rotational kinetic energy.
$$\eqalign{ & \therefore W = \frac{1}{2}I{\omega ^2} \cr & = \frac{1}{2}\left[ {{x^2} + 1.372 - 1.96x} \right]{\omega ^2} \cr} $$
For work done to be minimum
$$\eqalign{ & \frac{{dW}}{{dx}} = 0\,\,\,\,\, \Rightarrow 2x - 1.96 = 0 \cr & \Rightarrow x = \frac{{1.96}}{2} = 0.98\,m \cr} $$
The moment of inertia of the system about axis of rotation $$O$$ is

$$\eqalign{ & I = {I_1} + {I_2} = 0.3{x^2} + 0.7{\left( {1.4 - x} \right)^2} \cr & = 0.3{x^2} + 0.7\left( {1.96 + {x^2} - 2.8x} \right) \cr & = {x^2} + 1.372 - 1.96x \cr} $$
The work done in rotating the rod is converted into its rotational kinetic energy.
$$\eqalign{ & \therefore W = \frac{1}{2}I{\omega ^2} \cr & = \frac{1}{2}\left[ {{x^2} + 1.372 - 1.96x} \right]{\omega ^2} \cr} $$
For work done to be minimum
$$\eqalign{ & \frac{{dW}}{{dx}} = 0\,\,\,\,\, \Rightarrow 2x - 1.96 = 0 \cr & \Rightarrow x = \frac{{1.96}}{2} = 0.98\,m \cr} $$