Question
Two particles of mass $$m$$ each are tied at the ends of a light string of length $$2a.$$ The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance $$'a'$$ from the centre $$P$$ (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force $$F.$$ As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes $$2x,$$ is
A.
$$\frac{F}{{2m}}\frac{a}{{\sqrt {{a^2} - {x^2}} }}$$
B.
$$\frac{F}{{2m}}\frac{x}{{\sqrt {{a^2} - {x^2}} }}$$
C.
$$\frac{F}{{2m}}\frac{x}{a}$$
D.
$$\frac{F}{{2m}}\frac{{\sqrt {{a^2} - {x^2}} }}{x}$$
Answer :
$$\frac{F}{{2m}}\frac{x}{{\sqrt {{a^2} - {x^2}} }}$$
Solution :
The acceleration of mass $$m$$ is due to the force $$T\cos \theta $$
$$\eqalign{ & \therefore T\cos \theta = ma \Rightarrow a = \frac{{T\cos \theta }}{m}\,......\left( {\text{i}} \right) \cr & {\text{also, }}F = 2T\sin \theta \Rightarrow T = \frac{F}{{2\sin \theta }}......\left( {{\text{ii}}} \right) \cr} $$
From (i) and (ii)
$$\eqalign{ & a = \left( {\frac{F}{{2\sin \theta }}} \right)\frac{{\cos \theta }}{m} \cr & = \frac{F}{{2m\tan \theta }} = \frac{F}{{2m}}\frac{x}{{\sqrt {{a^2} - {x^2}} }}\,\,\left[ {\because \tan \theta \frac{{\sqrt {{a^2} - {x^2}} }}{x}} \right] \cr} $$
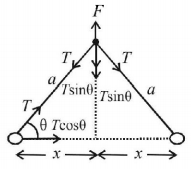
The acceleration of mass $$m$$ is due to the force $$T\cos \theta $$
$$\eqalign{ & \therefore T\cos \theta = ma \Rightarrow a = \frac{{T\cos \theta }}{m}\,......\left( {\text{i}} \right) \cr & {\text{also, }}F = 2T\sin \theta \Rightarrow T = \frac{F}{{2\sin \theta }}......\left( {{\text{ii}}} \right) \cr} $$
From (i) and (ii)
$$\eqalign{ & a = \left( {\frac{F}{{2\sin \theta }}} \right)\frac{{\cos \theta }}{m} \cr & = \frac{F}{{2m\tan \theta }} = \frac{F}{{2m}}\frac{x}{{\sqrt {{a^2} - {x^2}} }}\,\,\left[ {\because \tan \theta \frac{{\sqrt {{a^2} - {x^2}} }}{x}} \right] \cr} $$