Question
Two particles of equal mass $$'m'$$ go around a circle of radius $$R$$ under the action of their mutual gravitational attraction. The speed of each particle with respect to their centre of mass is
A.
$$\sqrt {\frac{{Gm}}{{4R}}} $$
B.
$$\sqrt {\frac{{Gm}}{{3R}}} $$
C.
$$\sqrt {\frac{{Gm}}{{2R}}} $$
D.
$$\sqrt {\frac{{Gm}}{R}} $$
Answer :
$$\sqrt {\frac{{Gm}}{{4R}}} $$
Solution :
Here, centripetal force will be given by the gravitational force between the two particles.
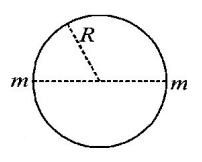
$$\eqalign{ & \frac{{G{m^2}}}{{{{\left( {2R} \right)}^2}}} = m{\omega ^2}R \cr & \Rightarrow \frac{{Gm}}{{4{R^3}}} = {\omega ^2} \Rightarrow \omega = \sqrt {\frac{{Gm}}{{4{R^3}}}} \cr} $$
If the velocity of the two particles with respect to the centre of gravity is $$v$$ then $$v = \omega R$$
$$v = \sqrt {\frac{{Gm}}{{4{R^3}}}} \times R = \sqrt {\frac{{Gm}}{{4R}}} $$
Here, centripetal force will be given by the gravitational force between the two particles.

$$\eqalign{ & \frac{{G{m^2}}}{{{{\left( {2R} \right)}^2}}} = m{\omega ^2}R \cr & \Rightarrow \frac{{Gm}}{{4{R^3}}} = {\omega ^2} \Rightarrow \omega = \sqrt {\frac{{Gm}}{{4{R^3}}}} \cr} $$
If the velocity of the two particles with respect to the centre of gravity is $$v$$ then $$v = \omega R$$
$$v = \sqrt {\frac{{Gm}}{{4{R^3}}}} \times R = \sqrt {\frac{{Gm}}{{4R}}} $$