Question
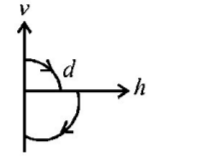
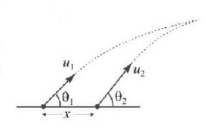
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
A.
$$\frac{{x\sin {\theta _2}}}{{{u_1}}}$$
B.
$$\frac{{x\cos {\theta _2}}}{{{u_2}}}$$
C.
$$\frac{{x\sin {\theta _2}}}{{{u_1}\sin \left( {{\theta _2} - {\theta _1}} \right)}}$$
D.
$$\frac{{x\sin {\theta _1}}}{{{u_2}\sin \left( {{\theta _2} - {\theta _1}} \right)}}$$
Answer :
$$\frac{{x\sin {\theta _2}}}{{{u_1}\sin \left( {{\theta _2} - {\theta _1}} \right)}}$$
Solution :
$$\eqalign{ & x + {u_2}\cos {\theta _2}t = {u_1}\cos {\theta _1}t \cr & \therefore t = \frac{x}{{{u_1}\cos {\theta _1} - {u_2}\cos {\theta _2}}}\,......\left( {\text{i}} \right) \cr} $$
Also $${u_1}\sin {\theta _1} = {u_2}\sin {\theta _2}\,......\left( {{\text{ii}}} \right)$$
After solving above equations, we get
$$t = \frac{{x\sin {\theta _2}}}{{{u_1}\sin \left( {{\theta _2} - {\theta _1}} \right)}}.$$
$$\eqalign{ & x + {u_2}\cos {\theta _2}t = {u_1}\cos {\theta _1}t \cr & \therefore t = \frac{x}{{{u_1}\cos {\theta _1} - {u_2}\cos {\theta _2}}}\,......\left( {\text{i}} \right) \cr} $$
Also $${u_1}\sin {\theta _1} = {u_2}\sin {\theta _2}\,......\left( {{\text{ii}}} \right)$$
After solving above equations, we get
$$t = \frac{{x\sin {\theta _2}}}{{{u_1}\sin \left( {{\theta _2} - {\theta _1}} \right)}}.$$