Two masses $$m$$ and $$\frac{m}{2}$$ are connected at the two ends of a massless rigid rod of length $$l.$$ The rod is suspended by a thin wire of torsional constant $$k$$ at the centre of mass of the rod-mass system (see figure). Because of torsional constant $$k,$$ the restoring toruque is $$\tau = k\theta $$  for angular displacement $$\theta .$$ If the rod is rotated by $${\theta _0}$$ and released, the tension in it when it passes through its mean position will be:

Solution :
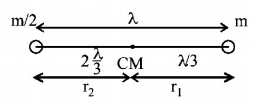
Distance of c.m from $$\frac{m}{2}$$
$$\eqalign{ & = \frac{{\frac{m}{2} \times 0 + m \times l}}{{\frac{m}{2} + m}} = \frac{{2l}}{3} \cr & {I_{cm}} = \frac{m}{2}{\left( {\frac{{2l}}{3}} \right)^2} + m{\left( {\frac{l}{3}} \right)^2} = \frac{1}{3}m{l^2} \cr} $$
At the mean position
$$\eqalign{ & \frac{1}{2}{I_{cm}}{\omega ^2} = \frac{1}{2}k\theta _0^2 \cr & \therefore {\omega ^2} = \frac{k}{{{I_{cm}}}}\theta _0^2 \cr & {\omega ^2} = \frac{{3k}}{{m{l^2}}}\theta _0^2 \cr} $$
As we know, $$\omega = \sqrt {\frac{k}{{{I_{cm}}}}} $$

Tension in the rod when it passes through the mean position,
$$ = m{\omega ^2}\frac{l}{3} = m\left[ {\frac{{3k}}{{m{l^2}}}\theta _0^2} \right]\frac{l}{3} = \frac{{k\theta _0^2}}{l}$$