Question
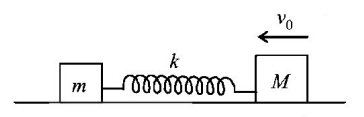
Two blocks of masses $$m$$ and $$M$$ are joined with an ideal spring of spring constant $$k$$ and kept on a rough surface as shown. The spring is initially unstretched and the coefficient of friction between the blocks and the horizontal surface is $$\mu .$$ What should be the maximum speed of the block of mass $$M$$ such that the smaller block does not move?
Two blocks of masses $$m$$ and $$M$$ are joined with an ideal spring of spring constant $$k$$ and kept on a rough surface as shown. The spring is initially unstretched and the coefficient of friction between the blocks and the horizontal surface is $$\mu .$$ What should be the maximum speed of the block of mass $$M$$ such that the smaller block does not move?
A.
$$\mu g\sqrt {\frac{{Mm}}{{\left( {M + m} \right)k}}} $$
B.
$$\mu g\sqrt {\frac{{\left( {M + m} \right)k}}{{Mm}}} $$
C.
$$\mu g\sqrt {\frac{{\left( {2M + m} \right)m}}{{km}}} $$
D.
None of these
Answer :
$$\mu g\sqrt {\frac{{\left( {2M + m} \right)m}}{{km}}} $$
Solution :
For the smaller block to move $$k{x_0} = \mu mg$$ and from work energy theorem
$$\eqalign{ & - \mu Mg{x_0} - \frac{1}{2}kx_0^2 = - \frac{1}{2}Mv_0^2 \cr & + \mu Mg\left( {\frac{{\mu mg}}{k}} \right) + \frac{1}{2}k{\left( {\frac{{\mu mg}}{k}} \right)^2} = \frac{1}{2}M{v^2} \cr & v = \mu g\sqrt {\frac{{\left( {2M + m} \right)m}}{{kM}}} \cr} $$
For the smaller block to move $$k{x_0} = \mu mg$$ and from work energy theorem
$$\eqalign{ & - \mu Mg{x_0} - \frac{1}{2}kx_0^2 = - \frac{1}{2}Mv_0^2 \cr & + \mu Mg\left( {\frac{{\mu mg}}{k}} \right) + \frac{1}{2}k{\left( {\frac{{\mu mg}}{k}} \right)^2} = \frac{1}{2}M{v^2} \cr & v = \mu g\sqrt {\frac{{\left( {2M + m} \right)m}}{{kM}}} \cr} $$