Question
Three resistances each of $$4\,\Omega $$ are connected to form a triangle. The resistance between any two terminals is
A.
$$12\,\Omega $$
B.
$$2\,\Omega $$
C.
$$6\,\Omega $$
D.
$$\frac{8}{3}\,\Omega $$
Answer :
$$\frac{8}{3}\,\Omega $$
Solution :
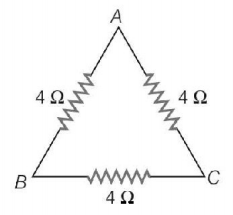
Between any two terminals, two resistors of two arms are in series i.e. between $$B$$ and $$C,$$ equivalent resistance is
$$\eqalign{ & \frac{1}{{{R_{BC}}}} = \frac{1}{4} + \frac{1}{8} \cr & \frac{1}{{{R_{BC}}}} = \frac{{2 + 1}}{8} \cr & \therefore {R_{BC}} = \frac{8}{3}\Omega \cr} $$

Between any two terminals, two resistors of two arms are in series i.e. between $$B$$ and $$C,$$ equivalent resistance is
$$\eqalign{ & \frac{1}{{{R_{BC}}}} = \frac{1}{4} + \frac{1}{8} \cr & \frac{1}{{{R_{BC}}}} = \frac{{2 + 1}}{8} \cr & \therefore {R_{BC}} = \frac{8}{3}\Omega \cr} $$