Question
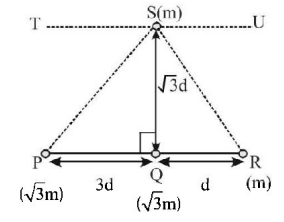
Three particles $$P,Q$$ and $$R$$ are placed as per given figure. Masses of $$P,Q$$ and $$R$$ are $$\sqrt 3 m,\sqrt 3 m$$ and $$m$$ respectively. The gravitational force on a fourth particle $$S$$ of mass $$m$$ is equal to
Three particles $$P,Q$$ and $$R$$ are placed as per given figure. Masses of $$P,Q$$ and $$R$$ are $$\sqrt 3 m,\sqrt 3 m$$ and $$m$$ respectively. The gravitational force on a fourth particle $$S$$ of mass $$m$$ is equal to
A.
$$\frac{{\sqrt 3 G{M^2}}}{{2{d^2}}}$$ in $$ST$$ direction only
B.
$$\frac{{\sqrt 3 G{M^2}}}{{2{d^2}}}$$ in $$SQ$$ direction and $$\frac{{\sqrt 3 G{M^2}}}{{2{d^2}}}$$ in $$SU$$ direction
C.
$$\frac{{\sqrt 3 G{M^2}}}{{2{d^2}}}$$ in $$SQ$$ direction only
D.
$$\frac{{\sqrt 3 G{M^2}}}{{2{d^2}}}$$ in $$SQ$$ direction and $$\frac{{\sqrt 3 G{M^2}}}{{2{d^2}}}$$ in $$ST$$ direction
Answer :
$$\frac{{\sqrt 3 G{M^2}}}{{2{d^2}}}$$ in $$SQ$$ direction only
Solution :
In horizontal direction
$$\eqalign{ & {\text{Net}}\,{\text{force}} = \frac{{G\sqrt 3 mm}}{{12{d^2}}}\cos {30^ \circ } - \frac{{G{m^2}}}{{4{d^2}}}\cos {60^ \circ } \cr & = \frac{{G{m^2}}}{{8{d^2}}} - \frac{{G{m^2}}}{{8{d^2}}} = 0 \cr} $$
In vertical direction,
$$\eqalign{ & {\text{Net}}\,{\text{force}} = \frac{{G\sqrt 3 {m^2}}}{{12{d^2}}}\cos {60^ \circ } + \frac{{G\sqrt 3 {m^2}}}{{3{d^2}}} + \frac{{G{m^2}}}{{4d}}\cos {30^ \circ } \cr & = \frac{{\sqrt 3 G{m^2}}}{{24{d^2}}} + \frac{{\sqrt 3 G{m^2}}}{{3{d^2}}} + \frac{{\sqrt 3 G{m^2}}}{{8{d^2}}} \cr & = \frac{{\sqrt 3 G{m^2}}}{{{d^2}}}\left[ {\frac{{1 + 8 + 3}}{{24}}} \right] = \frac{{\sqrt 3 G{m^2}}}{{2{d^2}}}\,{\text{along}}\,SQ. \cr} $$
In horizontal direction
$$\eqalign{ & {\text{Net}}\,{\text{force}} = \frac{{G\sqrt 3 mm}}{{12{d^2}}}\cos {30^ \circ } - \frac{{G{m^2}}}{{4{d^2}}}\cos {60^ \circ } \cr & = \frac{{G{m^2}}}{{8{d^2}}} - \frac{{G{m^2}}}{{8{d^2}}} = 0 \cr} $$
In vertical direction,
$$\eqalign{ & {\text{Net}}\,{\text{force}} = \frac{{G\sqrt 3 {m^2}}}{{12{d^2}}}\cos {60^ \circ } + \frac{{G\sqrt 3 {m^2}}}{{3{d^2}}} + \frac{{G{m^2}}}{{4d}}\cos {30^ \circ } \cr & = \frac{{\sqrt 3 G{m^2}}}{{24{d^2}}} + \frac{{\sqrt 3 G{m^2}}}{{3{d^2}}} + \frac{{\sqrt 3 G{m^2}}}{{8{d^2}}} \cr & = \frac{{\sqrt 3 G{m^2}}}{{{d^2}}}\left[ {\frac{{1 + 8 + 3}}{{24}}} \right] = \frac{{\sqrt 3 G{m^2}}}{{2{d^2}}}\,{\text{along}}\,SQ. \cr} $$