Question
The supply voltage to room is $$120V.$$ The resistance of the lead wires is $$6\Omega .A\,60 W$$ bulb is already switched on. What is the decrease of voltage across the bulb, when a $$240\,W$$ heater is switched on in parallel to the bulb?
A.
zero
B.
$$2.9\,Volt$$
C.
$$13.3\,Volt$$
D.
$$10.04\,Volt$$
Answer :
$$10.04\,Volt$$
Solution :
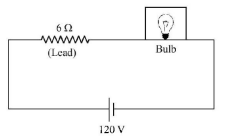
Power of bulb $$= 60\,W$$ (given)
Resistance of bulb = $$\frac{{120 \times 120}}{{60}} = 240\Omega \,\,\left[ {\because P = \frac{{{V^2}}}{R}} \right]$$
Power of heater $$= 240W$$ (given)
Resistance of heater = $$\frac{{120 \times 120}}{{240}} = 60\Omega $$
Voltage across bulb before heater is switched on, $${V_1} = \frac{{240}}{{246}} \times 120 = 117.73\,volt$$
Voltage across bulb after heater is switched on, $${V_2} = \frac{{48}}{{54}} \times 120 = 106.66\,volt$$
Hence decrease in voltage
$${V_1} - {V_2} = 117.73 - 106.66 = 10.04\,Volt\left( {{\text{approximately}}} \right)$$

Power of bulb $$= 60\,W$$ (given)
Resistance of bulb = $$\frac{{120 \times 120}}{{60}} = 240\Omega \,\,\left[ {\because P = \frac{{{V^2}}}{R}} \right]$$
Power of heater $$= 240W$$ (given)
Resistance of heater = $$\frac{{120 \times 120}}{{240}} = 60\Omega $$
Voltage across bulb before heater is switched on, $${V_1} = \frac{{240}}{{246}} \times 120 = 117.73\,volt$$
Voltage across bulb after heater is switched on, $${V_2} = \frac{{48}}{{54}} \times 120 = 106.66\,volt$$
Hence decrease in voltage
$${V_1} - {V_2} = 117.73 - 106.66 = 10.04\,Volt\left( {{\text{approximately}}} \right)$$