Question
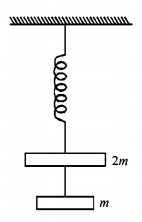
The string between blocks of mass $$m$$ and $$2m$$ is massless and inextensible. The system is suspended by a massless spring as shown. If the string is cut find the magnitudes of accelerations of mass $$2m$$ and $$m$$ (immediately after cutting)
The string between blocks of mass $$m$$ and $$2m$$ is massless and inextensible. The system is suspended by a massless spring as shown. If the string is cut find the magnitudes of accelerations of mass $$2m$$ and $$m$$ (immediately after cutting)
A.
g, g
B.
$$g,\frac{g}{2}$$
C.
$$\frac{g}{2},g$$
D.
$$\frac{g}{2},\frac{g}{2}$$
Answer :
$$\frac{g}{2},g$$
Solution :
In situation 1, the tension $$T$$ has to hold both the masses $$2m$$ and $$m$$ therefore,
$$T = 3mg$$
In situation 2, when the string is cut, the mass $$m$$ is a freely falling body and its acceleration due to gravity is $$g.$$
For mass $$2m,$$ just after the string is cut, $$T$$ remains $$3mg$$ because of the extension of string.
$$\therefore 3mg - 2mg = 2m \times a\,\,\,\,\therefore \frac{g}{2} = a$$
In situation 1, the tension $$T$$ has to hold both the masses $$2m$$ and $$m$$ therefore,
$$T = 3mg$$
In situation 2, when the string is cut, the mass $$m$$ is a freely falling body and its acceleration due to gravity is $$g.$$
For mass $$2m,$$ just after the string is cut, $$T$$ remains $$3mg$$ because of the extension of string.
$$\therefore 3mg - 2mg = 2m \times a\,\,\,\,\therefore \frac{g}{2} = a$$