Question
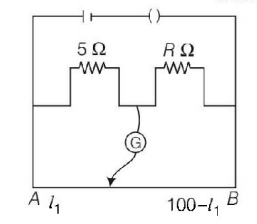
The resistances in the two arms of the meter bridge are $$5\,\Omega $$ and $$R\,\Omega ,$$ respectively. When the resistance $$R$$ is shunted with an equal resistance, the new balance point is at $$1.6\,{l_1}.$$ The resistance $$R,$$ is
The resistances in the two arms of the meter bridge are $$5\,\Omega $$ and $$R\,\Omega ,$$ respectively. When the resistance $$R$$ is shunted with an equal resistance, the new balance point is at $$1.6\,{l_1}.$$ The resistance $$R,$$ is
A.
$$10\,\Omega $$
B.
$$15\,\Omega $$
C.
$$20\,\Omega $$
D.
$$25\,\Omega $$
Answer :
$$15\,\Omega $$
Solution :
For first case, balanced condition of meter bridge will be
$$\frac{5}{{{l_1}}} = \frac{R}{{\left( {100 - {l_1}} \right)}}\,......\left( {\text{i}} \right)$$
Now, by shunting resistance $$R$$ by an equal resistance $$R,$$ new resistance in that arm become $$\frac{R}{2}.$$
So, new balanced condition will be
$$\frac{5}{{1.6{l_1}}} = \frac{{\frac{R}{2}}}{{\left( {100 - 1.6{l_1}} \right)}}\,......\left( {{\text{ii}}} \right)$$
From Eqs. (i) and (ii),
$$\eqalign{ & \frac{{1.6}}{1} = \frac{{\left( {100 - 1.6{l_1}} \right)}}{{100 - {l_1}}} \times 2 \cr & \Rightarrow 160 - 1.6{l_1} = 200 - 3.2{l_1} \cr & 1.6{l_1} = 40 \cr & {l_1} = \frac{{40}}{{1.6}} = 25\,m \cr & \Rightarrow {\text{From}}\,{\text{Eq}}{\text{.}}\left( {\text{i}} \right),\,\,\frac{5}{{25}} = \frac{R}{{75}} \Rightarrow R = 15\,\Omega \cr} $$
For first case, balanced condition of meter bridge will be
$$\frac{5}{{{l_1}}} = \frac{R}{{\left( {100 - {l_1}} \right)}}\,......\left( {\text{i}} \right)$$
Now, by shunting resistance $$R$$ by an equal resistance $$R,$$ new resistance in that arm become $$\frac{R}{2}.$$
So, new balanced condition will be
$$\frac{5}{{1.6{l_1}}} = \frac{{\frac{R}{2}}}{{\left( {100 - 1.6{l_1}} \right)}}\,......\left( {{\text{ii}}} \right)$$
From Eqs. (i) and (ii),
$$\eqalign{ & \frac{{1.6}}{1} = \frac{{\left( {100 - 1.6{l_1}} \right)}}{{100 - {l_1}}} \times 2 \cr & \Rightarrow 160 - 1.6{l_1} = 200 - 3.2{l_1} \cr & 1.6{l_1} = 40 \cr & {l_1} = \frac{{40}}{{1.6}} = 25\,m \cr & \Rightarrow {\text{From}}\,{\text{Eq}}{\text{.}}\left( {\text{i}} \right),\,\,\frac{5}{{25}} = \frac{R}{{75}} \Rightarrow R = 15\,\Omega \cr} $$