Question
The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is
A.
$$1:\sqrt 2 $$
B.
$$1:3$$
C.
$$2:1$$
D.
$$\sqrt 5 :\sqrt 6 $$
Answer :
$$\sqrt 5 :\sqrt 6 $$
Solution :
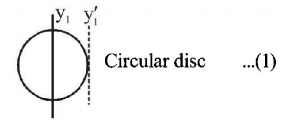
$$\eqalign{ & {I_{{y_1}}} = \frac{{M{R^2}}}{4} \cr & \therefore {{I'}_{{y_1}}} = \frac{{M{R^2}}}{4} + M{R^2} = \frac{5}{4}M{R^2} \cr} $$
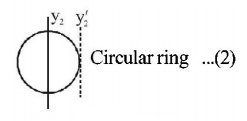
$$\eqalign{ & {I_{{y_2}}} = \frac{{M{R^2}}}{2} \cr & \therefore {{I'}_{{y_2}}} = \frac{{M{R^2}}}{2} + M{R^2} = \frac{3}{4}M{R^2} \cr & {{I'}_{{y_1}}} = MK_1^2,{{I'}_{{y_2}}} = MK_2^2 \cr & \therefore \frac{{K_1^2}}{{K_2^2}} = \frac{{{{I'}_{{y_1}}}}}{{{{I'}_{{y_2}}}}} \Rightarrow {K_1}:{K_2} = \sqrt 5 :\sqrt 6 \cr} $$

$$\eqalign{ & {I_{{y_1}}} = \frac{{M{R^2}}}{4} \cr & \therefore {{I'}_{{y_1}}} = \frac{{M{R^2}}}{4} + M{R^2} = \frac{5}{4}M{R^2} \cr} $$

$$\eqalign{ & {I_{{y_2}}} = \frac{{M{R^2}}}{2} \cr & \therefore {{I'}_{{y_2}}} = \frac{{M{R^2}}}{2} + M{R^2} = \frac{3}{4}M{R^2} \cr & {{I'}_{{y_1}}} = MK_1^2,{{I'}_{{y_2}}} = MK_2^2 \cr & \therefore \frac{{K_1^2}}{{K_2^2}} = \frac{{{{I'}_{{y_1}}}}}{{{{I'}_{{y_2}}}}} \Rightarrow {K_1}:{K_2} = \sqrt 5 :\sqrt 6 \cr} $$