Question
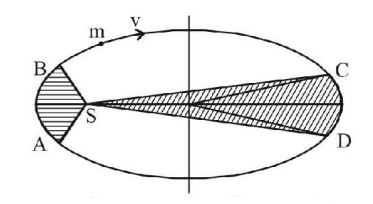
The figure shows elliptical orbit of a planet $$m$$ about the sun $$S.$$ The shaded area $$SCD$$ is twice the shaded area $$SAB.$$ If $${t_1}$$ is the time for the planet to move from $$C$$ to $$D$$ and $${t_2}$$ is the time to move from $$A$$ to $$B$$ then
The figure shows elliptical orbit of a planet $$m$$ about the sun $$S.$$ The shaded area $$SCD$$ is twice the shaded area $$SAB.$$ If $${t_1}$$ is the time for the planet to move from $$C$$ to $$D$$ and $${t_2}$$ is the time to move from $$A$$ to $$B$$ then
A.
$${t_1} = 4{t_2}$$
B.
$${t_1} = 2{t_2}$$
C.
$${t_1} = {t_2}$$
D.
$${t_1} > {t_2}$$
Answer :
$${t_1} = 2{t_2}$$
Solution :
According to Kepler’s law, the areal velocity of a planet around the sun always remains constant.
SCD : $${A_1} - {t_1}\,\left( {{\text{areal velocity constant}}} \right)$$
SAB : $${A_2} - {t_2}$$
$$\eqalign{ & \frac{{{A_1}}}{{{t_1}}} = \frac{{{A_2}}}{{{t_2}}},{t_1} = {t_2}.\frac{{{A_1}}}{{{A_2}}},\,\,\left( {{\text{given}}\,{A_1} = 2{A_2}} \right) \cr & = {t_2}.\frac{{2{A_2}}}{{{A_2}}} \cr & \therefore {t_1} = 2{t_2} \cr} $$
According to Kepler’s law, the areal velocity of a planet around the sun always remains constant.
SCD : $${A_1} - {t_1}\,\left( {{\text{areal velocity constant}}} \right)$$
SAB : $${A_2} - {t_2}$$
$$\eqalign{ & \frac{{{A_1}}}{{{t_1}}} = \frac{{{A_2}}}{{{t_2}}},{t_1} = {t_2}.\frac{{{A_1}}}{{{A_2}}},\,\,\left( {{\text{given}}\,{A_1} = 2{A_2}} \right) \cr & = {t_2}.\frac{{2{A_2}}}{{{A_2}}} \cr & \therefore {t_1} = 2{t_2} \cr} $$