Question
The degrees of freedom of a molecule of a triatomic gas are
A.
2
B.
4
C.
6
D.
8
Answer :
6
Solution :
The molecule of a triatomic gas has a tendency of rotating about any of three coordinate axes. So, it has 6 degrees of freedom, 3 translational and 3 rotational. At high enough temperature a triatomic molecule has 2 vibrational degree of freedom. But as temperature requirement is not given, so we answer simply by assuming triatomic gas molecule at room temperature.
Thus, $$f = 6$$
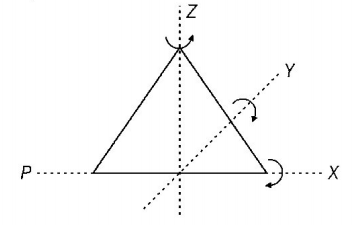
(3 translational +3 rotational) at room temperature.
The molecule of a triatomic gas has a tendency of rotating about any of three coordinate axes. So, it has 6 degrees of freedom, 3 translational and 3 rotational. At high enough temperature a triatomic molecule has 2 vibrational degree of freedom. But as temperature requirement is not given, so we answer simply by assuming triatomic gas molecule at room temperature.
Thus, $$f = 6$$

(3 translational +3 rotational) at room temperature.