Question
The bob of a simple pendulum executes simple harmonic motion in water with a period $$t,$$ while the period of oscillation of the bob is $${t_0}$$ in air. Neglecting frictional force of water and given that the density of the bob is $$\left( {\frac{4}{3}} \right) \times 1000\,kg/{m^3}.$$ What relationship between $$t$$ and $${t_0}$$ is true?
A.
$$t = {t_0}$$
B.
$$t = \frac{{{t_0}}}{2}$$
C.
$$t = 2{t_0}$$
D.
$$t = 4{t_0}$$
Answer :
$$t = 2{t_0}$$
Solution :
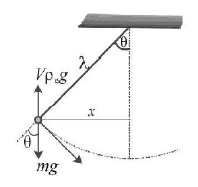
$${t_0} = 2\pi \sqrt {\frac{\ell }{g}} .$$
The restoring force in a liquid
$$\eqalign{ & F = - \left( {mg - V{\rho _e}g} \right)\sin \theta \cr & = - \left( {mg - \frac{m}{{\left( {\frac{4}{3} \times 1000} \right)}} \times 1000g} \right)\left( {\frac{x}{\ell }} \right) \cr & {\text{or}}\,\,a = \left( {g - \frac{{3g}}{4}} \right)\left( {\frac{{ - x}}{\ell }} \right) = \frac{g}{4}\left( {\frac{{ - x}}{\ell }} \right) \cr & \therefore t = 2\pi \sqrt {\frac{\ell }{{\left( {\frac{g}{4}} \right)}}} = 2{t_0}. \cr} $$

$${t_0} = 2\pi \sqrt {\frac{\ell }{g}} .$$
The restoring force in a liquid
$$\eqalign{ & F = - \left( {mg - V{\rho _e}g} \right)\sin \theta \cr & = - \left( {mg - \frac{m}{{\left( {\frac{4}{3} \times 1000} \right)}} \times 1000g} \right)\left( {\frac{x}{\ell }} \right) \cr & {\text{or}}\,\,a = \left( {g - \frac{{3g}}{4}} \right)\left( {\frac{{ - x}}{\ell }} \right) = \frac{g}{4}\left( {\frac{{ - x}}{\ell }} \right) \cr & \therefore t = 2\pi \sqrt {\frac{\ell }{{\left( {\frac{g}{4}} \right)}}} = 2{t_0}. \cr} $$