Question
The angle of incidence for a ray of light at a refracting surface of a prism is $${45^ \circ }.$$ The angle of prism is $${60^ \circ }.$$ If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are
A.
$${30^ \circ };\sqrt 2 $$
B.
$${45^ \circ };\sqrt 2 $$
C.
$${30^ \circ };\frac{1}{{\sqrt 2 }}$$
D.
$${45^ \circ };\frac{1}{{\sqrt 2 }}$$
Answer :
$${30^ \circ };\sqrt 2 $$
Solution :

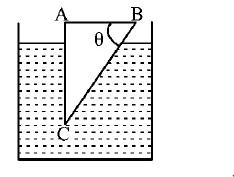
Consider a ray of light $$PQ$$ incident an the surface $$AB$$ and moves along $$RS,$$ after passing through the prism $$ABC.$$
It is given that the incident ray suffers minimum deviation. Therefore, the ray inside the prism must be parallel to the base $$BC$$ of the prism. From the geometry of the prism and the ray diagram, it is clear that
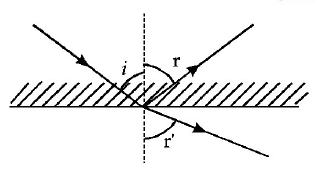
angle of incidence, $$i = {45^ \circ }$$
angle of refraction $$r = r' = {30^ \circ }$$
angle of emergence, $$e = {45^ \circ }$$
Therefore, minimum deviation suffered by the ray is
$${\delta _{\min }} = i + e - \left( {r + r'} \right) = {90^ \circ } - {60^ \circ } = {30^ \circ }$$
Also we know that
$$\mu = \frac{{\sin \left( {\frac{{A + {\delta _m}}}{2}} \right)}}{{\sin \frac{A}{2}}}$$
where, $$\mu =$$ refractive index of the material of the prism.
$$\eqalign{ & A = {\text{angle of prism}} = {60^ \circ } \cr & \therefore \mu = \frac{{\sin \left( {\frac{{{{60}^ \circ } + {{30}^ \circ }}}{2}} \right)}}{{\sin \frac{{{{60}^ \circ }}}{2}}} = \frac{{\sin {{45}^ \circ }}}{{\sin {{30}^ \circ }}} \cr & = \frac{{\frac{1}{{\sqrt 2 }}}}{{\frac{1}{2}}} = \frac{2}{{\sqrt 2 }} = \sqrt 2 \cr} $$

Consider a ray of light $$PQ$$ incident an the surface $$AB$$ and moves along $$RS,$$ after passing through the prism $$ABC.$$
It is given that the incident ray suffers minimum deviation. Therefore, the ray inside the prism must be parallel to the base $$BC$$ of the prism. From the geometry of the prism and the ray diagram, it is clear that
angle of incidence, $$i = {45^ \circ }$$
angle of refraction $$r = r' = {30^ \circ }$$
angle of emergence, $$e = {45^ \circ }$$
Therefore, minimum deviation suffered by the ray is
$${\delta _{\min }} = i + e - \left( {r + r'} \right) = {90^ \circ } - {60^ \circ } = {30^ \circ }$$
Also we know that
$$\mu = \frac{{\sin \left( {\frac{{A + {\delta _m}}}{2}} \right)}}{{\sin \frac{A}{2}}}$$
where, $$\mu =$$ refractive index of the material of the prism.
$$\eqalign{ & A = {\text{angle of prism}} = {60^ \circ } \cr & \therefore \mu = \frac{{\sin \left( {\frac{{{{60}^ \circ } + {{30}^ \circ }}}{2}} \right)}}{{\sin \frac{{{{60}^ \circ }}}{2}}} = \frac{{\sin {{45}^ \circ }}}{{\sin {{30}^ \circ }}} \cr & = \frac{{\frac{1}{{\sqrt 2 }}}}{{\frac{1}{2}}} = \frac{2}{{\sqrt 2 }} = \sqrt 2 \cr} $$