see the electrical circuit shown in this figure which of

See the electrical circuit shown in this figure. Which of the following equations is a correct equation for it?
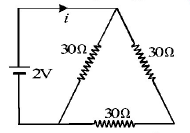
Electric Current mcq question image

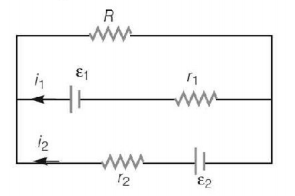
A. $${\varepsilon _1} - \left( {{i_1} + {i_2}} \right)R - {i_1}{r_1} = 0$$

B. $${\varepsilon _2} - {i_2}{r_2} - {\varepsilon _1} - {i_1}{r_1} = 0$$

C. $$ - {\varepsilon _2} - \left( {{i_1} + {i_2}} \right)R + {i_2}{r_2} = 0$$

D. $${\varepsilon _1} - \left( {{i_1} + {i_2}} \right)R + {i_1}{r_1} = 0$$

Answer : $${\varepsilon _1} - \left( {{i_1} + {i_2}} \right)R - {i_1}{r_1} = 0$$

Solution :
The algebraic sum of the changes in potential in complete transversal of a mesh (closed loop) is zero. i.e. $$\Sigma V = 0$$
So, $${\varepsilon _1} - \left( {{i_1} + {i_2}} \right)R - {i_1}{r_1} = 0$$

Releted MCQ Question on
Electrostatics and Magnetism >> Electric Current

Releted Question 1

The temperature coefficient of resistance of a wire is 0.00125 per $$^ \circ C$$ At $$300\,K,$$ its resistance is $$1\,ohm.$$ This resistance of the wire will be $$2\,ohm$$ at.

A. $$1154\,K$$

B. $$1100\,K$$

C. $$1400\,K$$

D. $$1127\,K$$

View Answer

Releted Question 2

A constant voltage is applied between the two ends of a uniform metallic wire. Some heat is developed in it. The heat developed is doubled if

A. both the length and the radius of the wire are halved.

B. both the length and the radius of the wire are doubled.

C. the radius of the wire is doubled.

D. the length of the wire is doubled.

View Answer

Releted Question 3

The electrostatic field due to a point charge depends on the distance $$r$$ as $$\frac{1}{{{r^2}}}.$$ Indicate which of the following quantities shows same dependence on $$r.$$

A. Intensity of light from a point source.

B. Electrostatic potential due to a point charge.

C. Electrostatic potential at a distance r from the centre of a charged metallic sphere. Given $$r$$ < radius of the sphere.

D. None of these

View Answer

Releted Question 4

The current $$i$$ in the circuit (see Fig) is

A. $$\frac{1}{{45}}A$$

B. $$\frac{1}{{15}}A$$

C. $$\frac{1}{{10}}A$$

D. $$\frac{1}{5}A$$

View Answer

See the electrical circuit shown in this figure. Which of the following equations is a correct equation for it?

Releted MCQ Question on
Electrostatics and Magnetism >> Electric Current

The temperature coefficient of resistance of a wire is 0.00125 per $$^ \circ C$$ At $$300\,K,$$ its resistance is $$1\,ohm.$$ This resistance of the wire will be $$2\,ohm$$ at.

A constant voltage is applied between the two ends of a uniform metallic wire. Some heat is developed in it. The heat developed is doubled if

The electrostatic field due to a point charge depends on the distance $$r$$ as $$\frac{1}{{{r^2}}}.$$ Indicate which of the following quantities shows same dependence on $$r.$$

The current $$i$$ in the circuit (see Fig) is

Practice More Releted MCQ Question on
Electric Current

Practice More MCQ Question on Physics Section

See the electrical circuit shown in this figure. Which of the following equations is a correct equation for it?

Releted MCQ Question on Electrostatics and Magnetism >> Electric Current

The temperature coefficient of resistance of a wire is 0.00125 per $$^ \circ C$$ At $$300\,K,$$ its resistance is $$1\,ohm.$$ This resistance of the wire will be $$2\,ohm$$ at.

A constant voltage is applied between the two ends of a uniform metallic wire. Some heat is developed in it. The heat developed is doubled if

The electrostatic field due to a point charge depends on the distance $$r$$ as $$\frac{1}{{{r^2}}}.$$ Indicate which of the following quantities shows same dependence on $$r.$$

The current $$i$$ in the circuit (see Fig) is

Practice More Releted MCQ Question on Electric Current

Practice More MCQ Question on Physics Section

Releted MCQ Question on
Electrostatics and Magnetism >> Electric Current

Practice More Releted MCQ Question on
Electric Current