Question
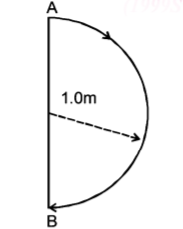
$$P$$ is the point of contact of a wheel and the ground. The radius of wheel is $$1\,m.$$ The wheel rolls on the ground without slipping. The displacement of point $$P$$ when wheel completes half rotation is
A.
$$2m$$
B.
$$\sqrt {{\pi ^2} + 4} m$$
C.
$$\pi m$$
D.
$$\sqrt {{\pi ^2} + 2} m$$
Answer :
$$\sqrt {{\pi ^2} + 4} m$$
Solution :
When the wheel rolls on the ground without slipping and completes half rotation, point $$P$$ takes new position as $$P’$$ as shown in figure.
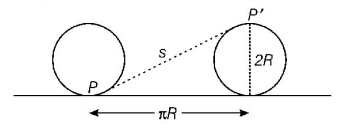
Horizontal displacement, $$x = \pi R$$
Vertical displacement, $$y = 2R$$
Thus, displacement of the point $$P$$ when wheel completes half rotation,
$$\eqalign{ & s = \sqrt {{x^2} + {y^2}} \cr & = \sqrt {{{\left( {\pi R} \right)}^2} + {{\left( {2R} \right)}^2}} \cr & = \sqrt {{\pi ^2}{R^2} + 4{R^2}} \cr & {\text{but}}\,R = 1\,m\,\,\left( {{\text{given}}} \right) \cr & \therefore s = \sqrt {{\pi ^2}{{\left( 1 \right)}^2} + 4{{\left( 1 \right)}^2}} \cr & = \sqrt {{\pi ^2} + 4} \,m \cr} $$
When the wheel rolls on the ground without slipping and completes half rotation, point $$P$$ takes new position as $$P’$$ as shown in figure.

Horizontal displacement, $$x = \pi R$$
Vertical displacement, $$y = 2R$$
Thus, displacement of the point $$P$$ when wheel completes half rotation,
$$\eqalign{ & s = \sqrt {{x^2} + {y^2}} \cr & = \sqrt {{{\left( {\pi R} \right)}^2} + {{\left( {2R} \right)}^2}} \cr & = \sqrt {{\pi ^2}{R^2} + 4{R^2}} \cr & {\text{but}}\,R = 1\,m\,\,\left( {{\text{given}}} \right) \cr & \therefore s = \sqrt {{\pi ^2}{{\left( 1 \right)}^2} + 4{{\left( 1 \right)}^2}} \cr & = \sqrt {{\pi ^2} + 4} \,m \cr} $$