Question
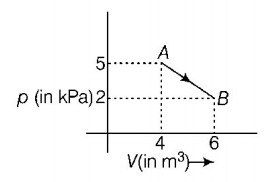
One mole of an ideal diatomic gas undergoes a transition from $$A$$ to $$B$$ along a path $$AB$$ as shown in the figure.
One mole of an ideal diatomic gas undergoes a transition from $$A$$ to $$B$$ along a path $$AB$$ as shown in the figure.
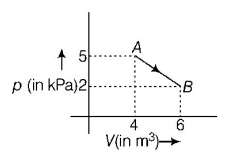
The change in internal energy of the gas during the transition is
A.
$$20\,kJ$$
B.
$$-20\,kJ$$
C.
$$20\,J$$
D.
$$-12\,kJ$$
Answer :
$$-20\,kJ$$
Solution :
For a diatomic gas,
$${C_V} = \frac{5}{2}R$$
The change in internal energy of gas in the transition from $$A$$ to $$B$$ is
$$\eqalign{ & \Delta U = n{C_V}dT \cr & = n\left( {\frac{{5R}}{2}} \right)\left( {{T_B} - {T_A}} \right) \cr & = nR\frac{5}{2}\left( {\frac{{{p_B}{V_B}}}{{nR}} - \frac{{{p_A}{V_A}}}{{nR}}} \right) \cr & = \frac{5}{2}\left( {2 \times {{10}^3} \times 6 - 5 \times {{10}^3} \times 4} \right) \cr & = \frac{5}{2} \times \left( { - 8 \times {{10}^3}} \right) \cr & = - \frac{{4 \times {{10}^4}}}{2} = - 20\,kJ \cr} $$
For a diatomic gas,

$${C_V} = \frac{5}{2}R$$
The change in internal energy of gas in the transition from $$A$$ to $$B$$ is
$$\eqalign{ & \Delta U = n{C_V}dT \cr & = n\left( {\frac{{5R}}{2}} \right)\left( {{T_B} - {T_A}} \right) \cr & = nR\frac{5}{2}\left( {\frac{{{p_B}{V_B}}}{{nR}} - \frac{{{p_A}{V_A}}}{{nR}}} \right) \cr & = \frac{5}{2}\left( {2 \times {{10}^3} \times 6 - 5 \times {{10}^3} \times 4} \right) \cr & = \frac{5}{2} \times \left( { - 8 \times {{10}^3}} \right) \cr & = - \frac{{4 \times {{10}^4}}}{2} = - 20\,kJ \cr} $$