Question
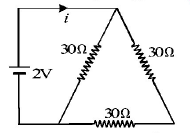
In the network shown below, the ring has zero resistance. The equivalent resistance between the point $$A$$ and $$B$$ is
In the network shown below, the ring has zero resistance. The equivalent resistance between the point $$A$$ and $$B$$ is

A.
$$2R$$
B.
$$4R$$
C.
$$7R$$
D.
$$10R$$
Answer :
$$2R$$
Solution :
As the ring has no resistance, the three resistances of $$3R$$ each are in parallel.
$$\eqalign{ & \Rightarrow \frac{1}{{R'}} = \frac{1}{{3R}} + \frac{1}{{3R}} + \frac{1}{{3R}} = \frac{1}{R} \cr & \Rightarrow R' = R \cr} $$
$$\therefore $$ between point $$A$$ and $$B$$ equivalent resistance $$= R + R = 2R.$$
As the ring has no resistance, the three resistances of $$3R$$ each are in parallel.
$$\eqalign{ & \Rightarrow \frac{1}{{R'}} = \frac{1}{{3R}} + \frac{1}{{3R}} + \frac{1}{{3R}} = \frac{1}{R} \cr & \Rightarrow R' = R \cr} $$
$$\therefore $$ between point $$A$$ and $$B$$ equivalent resistance $$= R + R = 2R.$$